
В.И. Васюков, Ю.М. Дильдин, С.В. Ладов, С.В. Федоров
6
Инженерный журнал: наука и инновации
# 4·2017
2
2
2
2
2
2
2
2
1
1
1
1
1
ln
1 ln
1 .
4
R
R
R
R
J
R
R
R
R
=
−
−
−
(12)
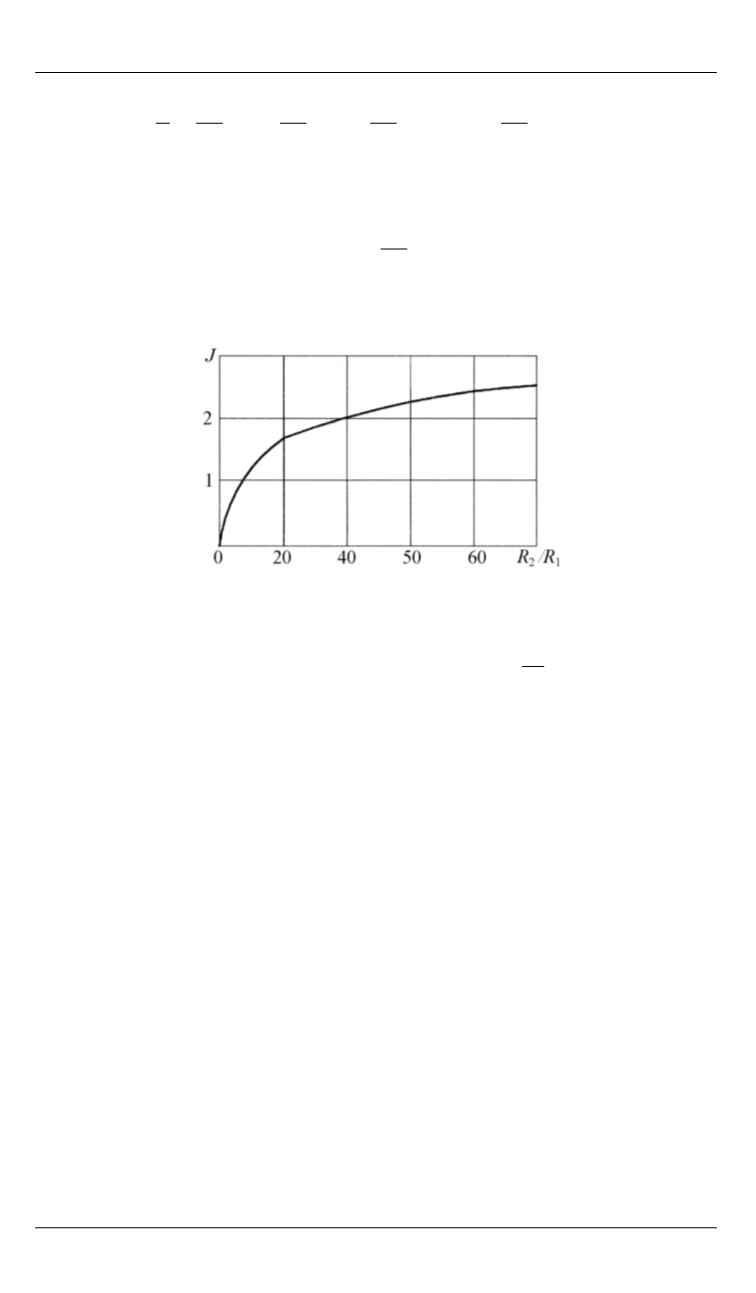
Для дальнейших расчетов значение интеграла (12) представим
графически в виде функции
2
1
R J J
R
=
(рис. 2).
Рис. 2.
Графическое представление интеграла
J
в виде функциональной зависимости
2
1
R
J J
R
=
В целях упрощения расчетов реальный криволинейный профиль
пробоины можно заменить ступенчатым и для каждой ступени
i
h
определить средний внутренний радиус пробоины
1
i
R
и средний
наружный радиус пробоины
2
i
R
деформированного цилиндра в рас-
сматриваемом сечении (см. рис. 1). Поэтому формулу для расчета
энергии кумулятивной струи, которая выделяется в
i
-м сечении ци-
линдрического образца, можно записать в виде
1
c
1
10 ,
i
i i
E Kh R J
−
=
⋅
(13)
где
c
i
E
— в джоулях;
K
= 49,25;
i
h
и
1
i
R
— в миллиметрах.
Полную энергию кумулятивной струи можно определить по ра-
венству
c
c
1
.
i
i n
i
E E
=
=
=
∑
















