Определение энергии кумулятивной струи различными способами

5 / 16

Определение энергии кумулятивной струи различными способами
Инженерный журнал: наука и инновации # 4·2017 5
2 2 ln
3 3 i
R
r ϕ ε = ε = , (7)
где R, r — радиусы деформированного и недеформированного ци-
линдрического образца соответственно.
Деформация стального цилиндра (рис. 1) отвечает уровню rdr =
= RdR, откуда с учетом принятых обозначений получаем соотноше-
ние
2 2 2
1 1 r R r R= + − . (8)
Подставив в выражение (5) соотношения (7), (8) и учитывая, что
т.д ,
i σ = σ где т.д σ — динамический предел текучести, получаем
2
1
т.д 2 2 2
1 1
4
ln .
3
R
R
R
E H R dR
R r R
π = σ
+ − ∫ (9)
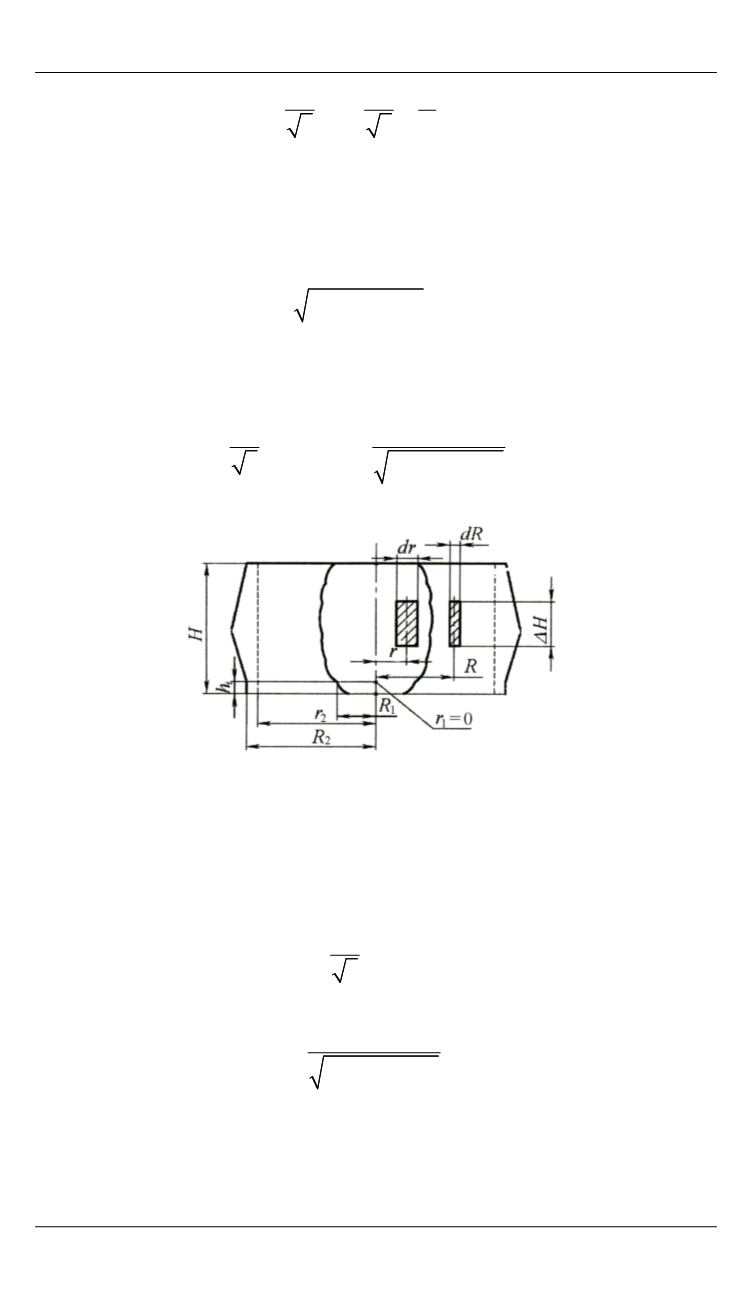
Рис. 1. Схема деформирования стального
цилиндра и радиального расширения про-
боины при проникании кумулятивной струи
Уравнение (9) представим в виде
т.д
4
,
3
E H J
π = σ
(10)
где
2
1
2 2 2
1 1
ln .
R
R
R
J R dR
R r R
=
+ − ∫ (11)
Выражение (11) можно проинтегрировать при условии, что
начальный радиус отверстия равен нулю ( 1 r = 0), тогда получаем со-
отношение