
Н.К. Веретимус, Д.К. Веретимус
4
Если значение коэффициента меньше нуля, то принимают
0.
nP
r
Постоянная в уравнении для скорости роста трещины
2
1 .
2
P
fP
C
e
(4)
Если принять, что значение функции
f
(
r
/
l
) = 1, уравнение скорости ро-
ста трещины [1, 2, 8, 9] без учета значений функции
f
(
r
/
l
)
2
имеет вид
I
I
I
I
1
,
1
K
K
P
P
dl C K
dN
C K l
(5)
где
I
1
2 .
K
keP
p
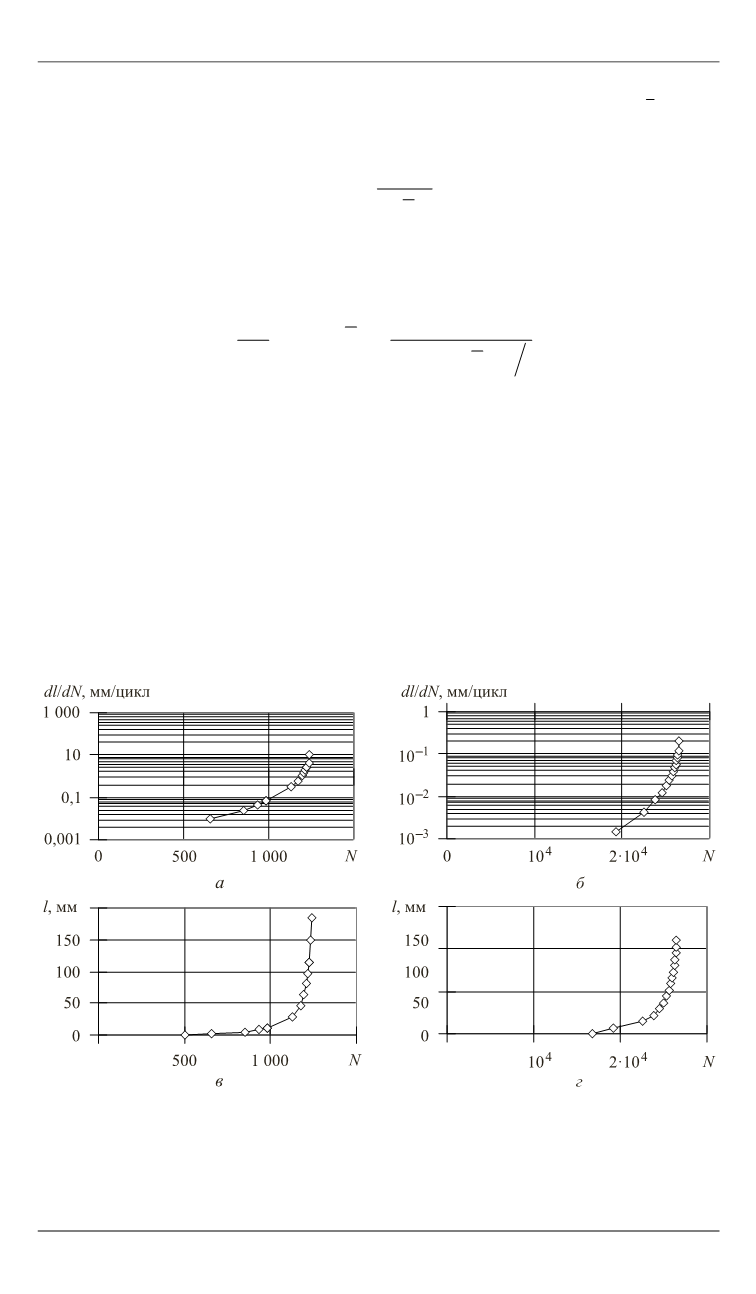
Зависимость скорости роста трещины от числа циклов для диска
[2, 11] (
n
= 17 500 об/мин,
t
= 20
C) и толстостенной трубы (
p
1
=
= 400 МПа,
t
= 20
C) при изотермическом нагружении представлена
на рис. 1. На рисунке видно, что и в диске при
N
>1 200 циклов, и
в трубе при
N
> 25 000 циклов скорость роста трещины резко возрас-
тает. Однако при числе циклов нагружения, близком к числу циклов
до разрушения, скорость прорастания трещины в диске приблизи-
тельно на два порядка выше, чем в толстостенной трубе.
Рис. 1.
Зависимость скорости прорастания трещины (
а
,
б
) и ее длины (
в
,
г
) от числа
циклов нагружения для диска (
а
,
в
) при
n
= 17500 об/мин,
t
= 20
C и толстостенной
трубы (
б
,
г
) при
p
1
= 400 МПа,
t
= 20
C
















