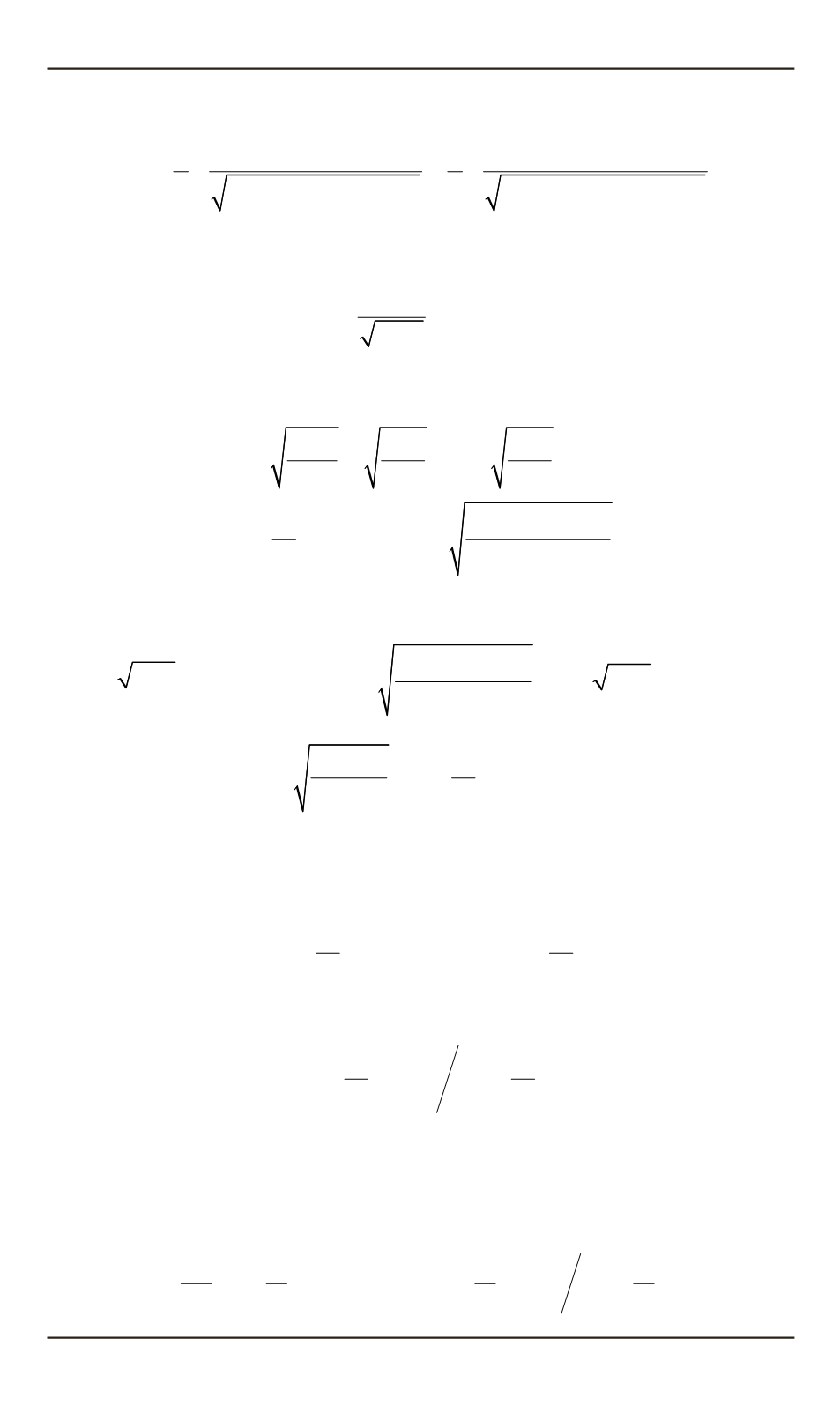
6
А.А. Гурченков, Д.В. Башкина, Н.Т. Вилисова
Второй из интегралов (8) вычислим аналогично:
(
)(
)
(
)(
)(
)
2
2
2
1
1
1
.
2
2
1
1
u
u
b
du
du
q
u
u u
a u b u u c
−
=
=
− + + ε +
− − −
∫
∫
Теперь, используя формулу (1.2.28) из [7], находим
(
)
2
2 2
1
,
,
q
F k
a c
=
ϕ
−
где
F
(φ,
k
) – неполный эллиптический интеграл первого рода [6],
(
)(
)
(
)(
)
2
2
2
2
2
2
2
1 ,
,
1
1
,
arcsin
.
a b
k
k
a c
a c u c
k
k
a b b c
−
ε
′
=
=
=
−
+ ε
+ ε
− −
⎛ ⎞′
ε =
ϕ =
⎜ ⎟
− −
⎝ ⎠
Из (3) следует, что
(
)
2
2 2
1
,
q F k
+ ε = ϕ
или
(
)(
)
(
)
2
2 2
2
1
1
sn 1 ,
,
1
u
q k
u
+ ε +
=
+ ε
+ + ε
2
2 2
2
2 2
2
1
1 sn
,
.
1
u
q k
k u
k
⎛
⎞
+
= ⎜
⎟
+ ⎝
⎠
Выполнив очевидные преобразования после возведения в квадрат
обеих частей этого уравнения:
2 2
2
2
2
2 2
2 2
2
2
1
1
1 sn
,
1 sn
,
,
u k
q k
q k
k
k
⎛
⎞ ⎛
⎞
⎛
⎞
⎛
⎞
−
= − −
⎜
⎟ ⎜
⎟
⎜
⎟
⎜
⎟
⎜
⎟ ⎜
⎟
⎝
⎠
⎝
⎠
⎝
⎠ ⎝
⎠
получаем
2
2
2
2 2
2 2
2
2
1
1
cn
,
dn
,
.
u
q k
q k
k
k
⎛
⎞
⎛
⎞
= − ⎜
⎟
⎜
⎟
⎝
⎠
⎝
⎠
Обратим внимание на то, что
k
1
=
k′
2
и
k′
1
=
k
2
. Это позволяет ввести
один общий модуль
k
эллиптических функций.
Связьмежду координатами (
u
1
,
u
2
) и (
q
1
,
q
2
) определяетсяформулами
2
2
2
1
1
2
2
2
2
1
1
1
1
dn
, ,
cn
,
dn
,
;
u
q k u
q k
q k
k
k
k
k
⎛
⎞
⎛
⎞
⎛
⎞
′
′
= −
= − ⎜
⎟
⎜
⎟
⎜
⎟
′
′
′
′
⎝
⎠
⎝
⎠
⎝
⎠
(11)