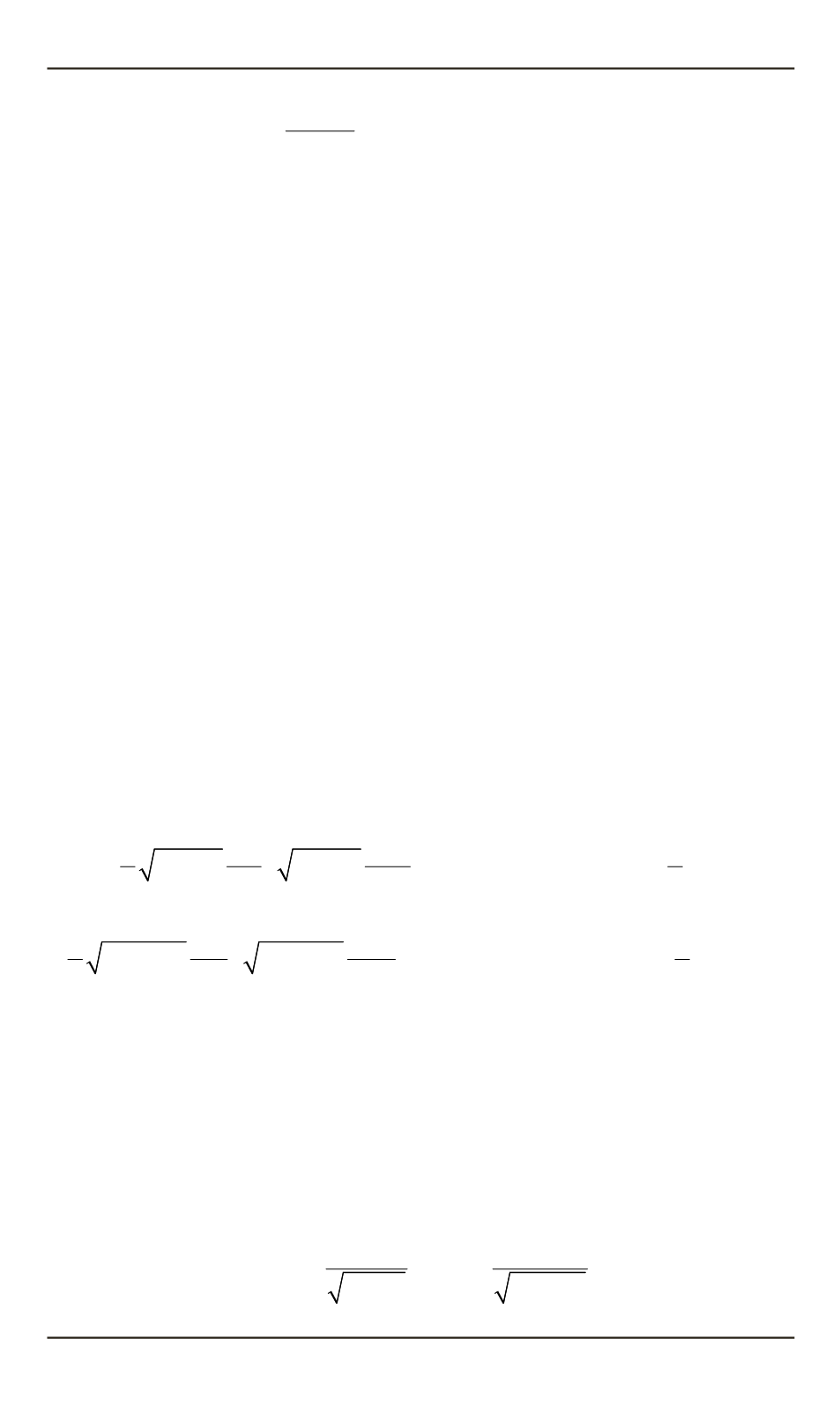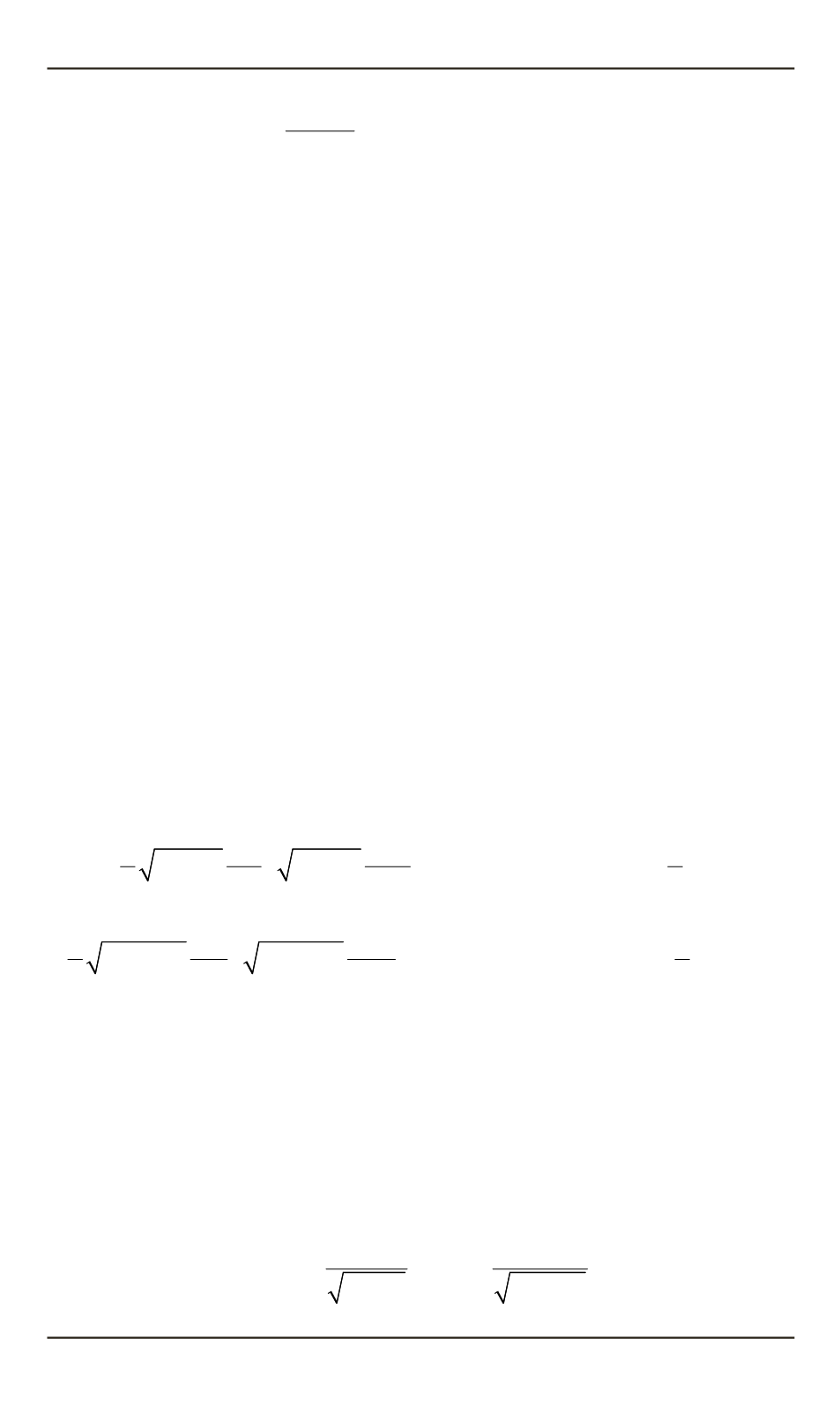
4
А.А. Гурченков, Д.В. Башкина, Н.Т. Вилисова
(
)
(
)
3
3
2
(2)
2
2
2 1
1 2
1
1 2
2
1
2
1 2
2 1
,
,
u u
U u u
u u u u u u u u
u u
−
=
= + + = + −
−
(4)
Таким образом, потенциалы
U
(1)
и
U
(2)
являются многочленами от
переменных
u
1
+
u
2
и
u
1
u
2
и, согласно соотношениям (3), (4), легко про-
должаются на всю единичную сферу. Отметим, что потенциал
(
)
(
)
(
)
(1)
(2)
1 2
1
1 2
2
1 2
,
,
,
,
U u u CU u u C U u u
=
+
(5)
являющийся линейной комбинацией потенциалов
U
(1)
и
U
(2)
, также до-
пускает разделение переменных. Без потери общности можно считать,
что
C
1
= 1.
В исходных переменных
( , , )
r x y z
=
G
потенциал
U
(
x
,
y
,
z
) (5) запи-
сывается так:
(
)
(
)
(
)
2
2
2
( , , )
,
,
1
.
z
U x y z
r A r
r A r
r
ε
ε
= α
+ β
− α + ε
G G
G G
Произвольные постоянные α, β определены соотношениями
(
)
2
1
2
,
2 2 ,
C C C
α = β = − +
+ ε
а диагональная матрица
A
ε
имеет вид
(
)
diag 1 , 1,0 .
A
ε
= − − − ε −
Для потенциала (5) уравнение Шредингера (1) записывается в виде
системы
2
3
1
1
1
1 1
1 1
2 1
1
1
1
1
1
4 ( )
4 ( )
;
2
2
d
d
f u
f u
Eu C u C u
du
du
⎛
⎞Ψ
−
+ Ψ − − = ΛΨ
⎜
⎟
⎝
⎠
(6)
2
3
2
2
2
2 2
1 2
2 2
2
2
2
1
1
4 ( )
4 ( )
,
2
2
d
d
f u
f u
Eu C u C u
du
du
⎛
⎞Ψ
− −
−
− Ψ + + = − ΛΨ
⎜
⎟
⎝
⎠
(7)
где
Λ
– константа разделения.
Таким образом, получена так называемая параметрическая задача
на собственные значения [4]. Здесь роль параметра играет
E
, а соб-
ственным значением является константа разделения
Λ
.
2. Переход к сфероконическим координатам.
От перемен-
ных (
u
1
,
u
2
) перейдем к новым переменным (
q
1
,
q
2
), определенных
соотношениями
1
2
1
2
1
1
,
.
4 ( )
4 ( )
u
u
du
du
q
q
f u
f u
− −ε
−
=
=
−
∫
∫
(8)