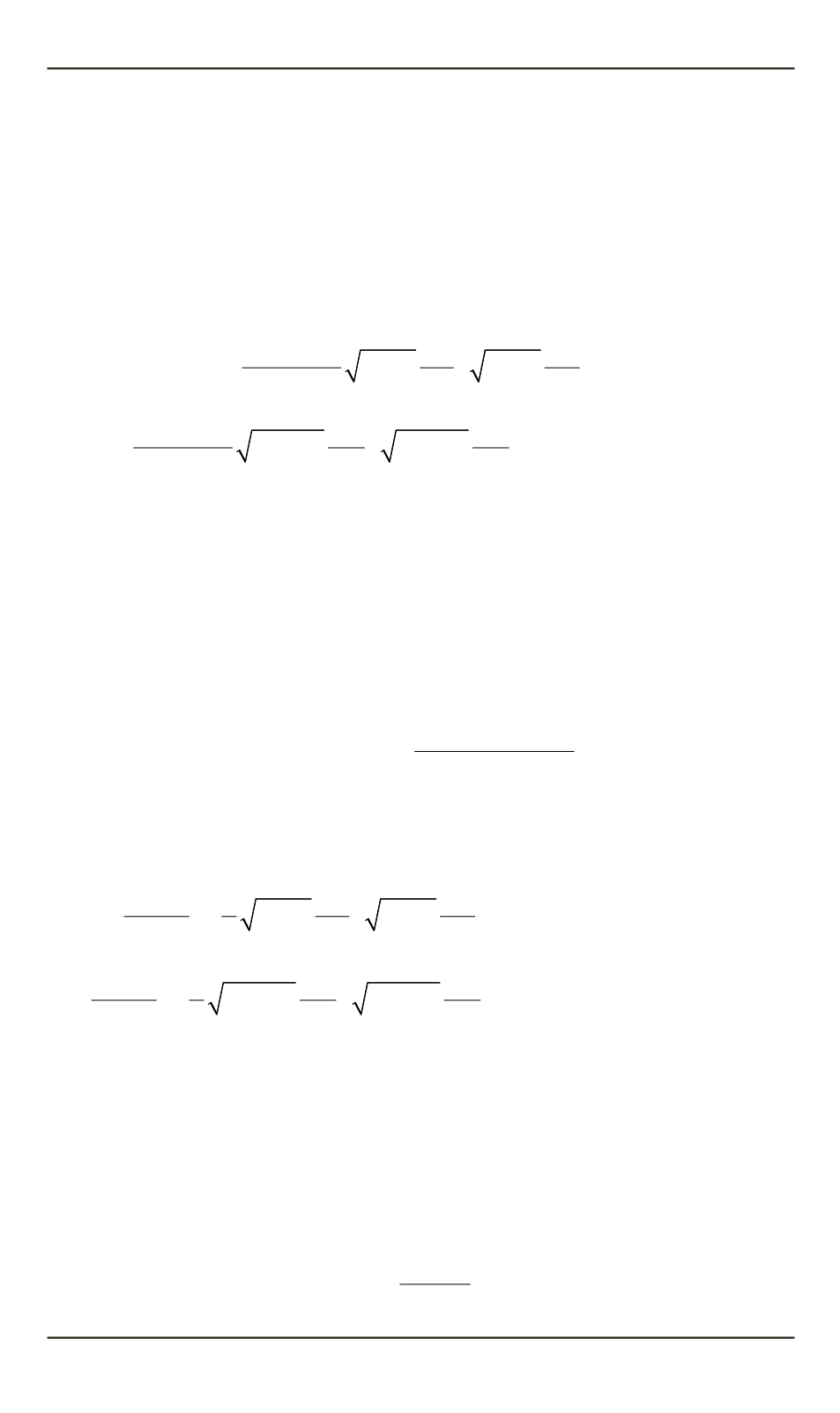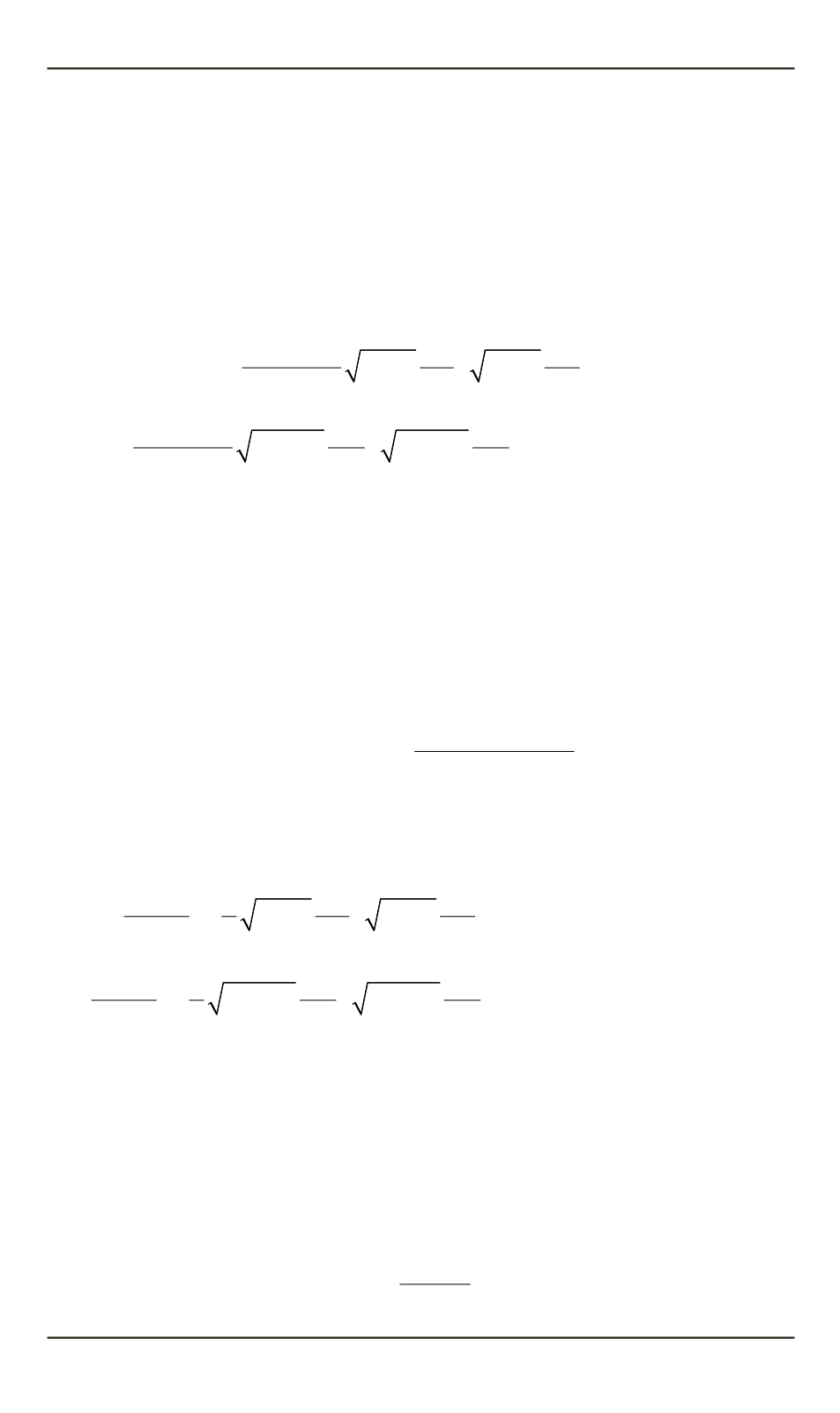
3
Энергетический спектр в одной задаче о квантовом ротаторе
1
2
1
1
0,
u
u
− − ε ≤ ≤ − ≤ ≤
который отображается на 1/8 единичной сферы. Координатные линии
u
1
= const и
u
2
= const, как будет показано ниже, совпадают с соответ-
ствующими координатными линиями конической системы координат,
которая иногда называется также сфероконической [5].
В этих новых переменных уравнение Шредингера записывается
следующим образом:
(
)
(
)
(
)
1
1
2 1
1
1
2
2
1 2
2 1
2
2
1
( )
( )
2
1
( )
( )
,
,
2
f u
f u
u u
u
u
f u
f u
U u u
E
u u
u
u
⎛
⎞
∂
∂Ψ
−
−
⎜
⎟
−
∂
∂
⎝
⎠
⎛
⎞
∂
∂Ψ
−
−
−
+
Ψ = Ψ
⎜
⎟
−
∂
∂
⎝
⎠
где
(
)(
)
( )
1
1 ,
f u u
u u
= + + ε +
причем
1
2
( ) 0, ( ) 0.
f u
f u
>
<
Теперь предположим, что потенциал
U
в новых переменных имеет
вид
(
)
( )
( )
2 2
1 1
1 2
2 1
,
,
U u U u
U U u u
u u
−
=
=
−
тогда переменные в уравнении Шредингера [1] разделяются. Действи-
тельно, в этом случае уравнение Шредингера записывается в виде
( )
(
)
( )
(
)
1
1
1
1 1
2 1
1
1
2
2
2
2 2
2 1
2
2
1 1 ( )
( )
2
1 1 ( )
( )
0,
2
f u
f u
Eu U u
u u
u
u
f u
f u
Eu U u
u u
u
u
⎛
⎞
⎛
⎞
∂
∂Ψ
−
+ −
Ψ +
⎜
⎟
⎜
⎟
⎜
⎟
−
∂
∂
⎝
⎠
⎝
⎠
⎛
⎞
⎛
⎞
∂
∂Ψ
+
− −
−
− −
Ψ =
⎜
⎟
⎜
⎟
⎜
⎟
−
∂
∂
⎝
⎠
⎝
⎠
(2)
допускающем разделение переменных
(
)
( ) ( )
1 2
1 1 2 2
,
.
u u
u u
Ψ = Ψ Ψ
Поскольку переменные (
u
1
,
u
2
) определены только на 1/8 части еди-
ничной сферы, необходимо иметь возможность продолжения их на
всю сферу. Этого можно добиться, например, взяв в качестве функций
U
1
(
u
1
) и
U
2
(
u
2
) соответственно функции
u
1
n
и
u
2
n
. Достаточно рассмо-
треть случаи, когда
n
= 2 и
n
= 3:
(
)
2
2
(1)
2
1
1 2
1
2
2 1
,
,
u u
U u u
u u
u u
−
=
= +
−
(3)