Ю.Н. Барышников
4
с зависимой задней подвеской (рис. 3,
кривая
2
), в 1,6 раза меньше, чем у ав-
томобиля с независимой задней под-
веской (рис. 3, кривая
1
).
Таким образом, одним из воз-
можных путей снижения кососим-
метричных нагрузок является приме-
нение зависимой задней подвески.
Этот вывод косвенно подтверждается
наличием такого типа подвесок у
многих зарубежных аналогов.
Другой расчетный случай — раз-
грузка карьерных самосвалов. В зави-
симости от расстояния до пункта раз-
грузки карьерные самосвалы в течение
суток совершают более двадцати по-
грузочно-разгрузочных операций, а за
весь период работы — свыше десяти
тысяч. Как показывает опыт эксплуа-
тации, такие режимы часто являются
одной из причин разрушения элемен-
тов несущей конструкции.
Расчетная схема карьерного са-
мосвала в процессе разгрузки плат-
формы представлена на рис. 4.
В ряде случаев, например, в меж-
сезонный или зимний период, когда горная масса слипается, при подъ-
еме платформы возможны два экстремальных режима. В первом случае
горная масса прилипает (примерзает) к днищу платформы; во втором —
вся горная масса приходит в движение после подъема платформы на
угол естественного откоса. Найдем силы, действующие на раму само-
свала в вышеуказанных случаях.
Обозначим
P
1
и
P
2
силы тяжести платформы и груза;
x
1
,
y
1
и
x
2
,
y
2
—
координаты центра масс платформы и груза;
— угол подъема
платформы;
—
угол наклона гидроцилиндра. Рассмотрим случай,
когда груз движется как монолитная глыба, симметричная относи-
тельно вертикальной плоскости
xОy
. Для расчета силы
Q
гидроци-
линдра и реакций
R
в шарнирных опорах платформы воспользуемся
принципом Даламбера. Приведем силы инерции груза к центру его
масс (точка
С
) в виде главного вектора
ин
R
и главного момента
ин
:
c
L
ин
2
,
C
R M a
где
M
2
и
a̅
C
— масса и ускорение центра масс груза;
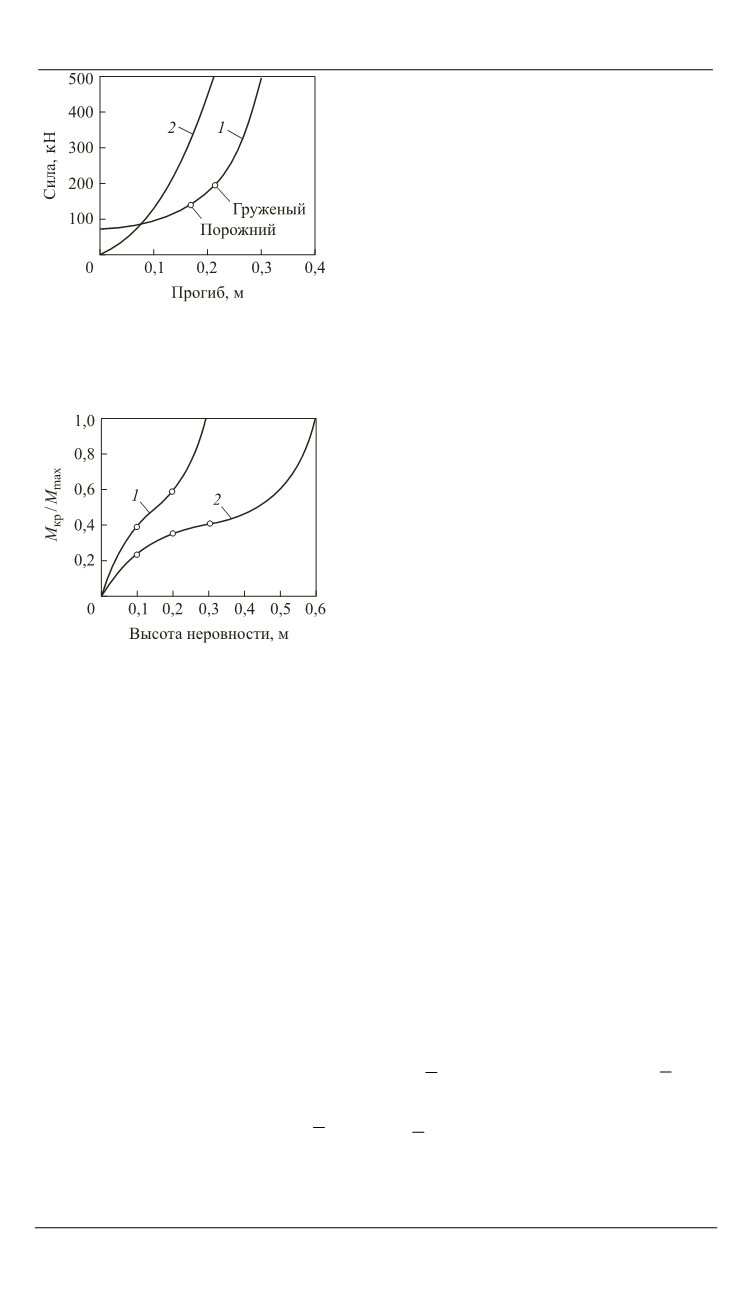
Рис. 3.
Зависимость крутящего
момента на раму от высоты не-
ровности
Рис. 2.
Упругие характеристики:
1
— передней подвески;
2
— пе-
редних шин


