А.А. Гурченков
2
ется по закону синуса, что соответствует равновероятному вылету
частиц с поверхности.
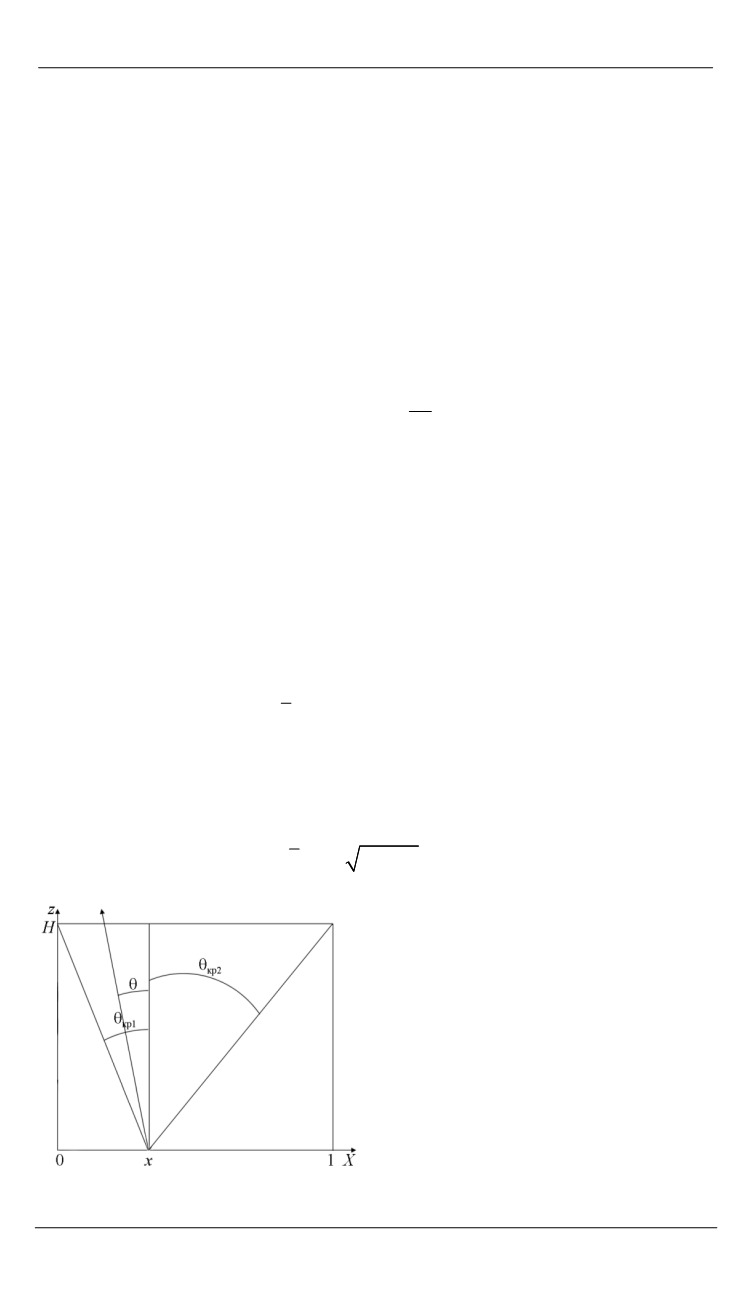
Следуя геометрико-вероятностному подходу, из схемы, пред-
ставленной на рисунке, получаем: точечная частица, имеющая коор-
динату
х
, может вылететь из системы с относительной высотой сте-
нок, равной
Н
, без столкновения со стенками в том случае, если со-
отношение между компонентами скоростей
v
x
и
v
y
будет таким, что
угол, под которым вылетает частица, будет меньше критических уг-
лов θ
кр1
и θ
кр2
.
Для произвольного положения
х
частицы на поверхности конден-
сированной фазы можно найти критический угол по формуле
кр1
=arctg .
x
H
Все частицы, вылетающие из точки с координатой
х
, могут выле-
теть из системы без столкновений со стенками, если угол вылета θ,
определяемый составляющими скорости, принадлежит интервалу (0;
θ
кр1
). Отсюда можно определить средний угол вылета частиц из систе-
мы, просуммировав все возможные углы вылета θ и все возможные
положения точек вылета на поверхности конденсированной фазы от
нуля до единицы. Средний критический угол для вылета частиц по за-
кону косинуса будет определяться с помощью двойного интеграла:
кр1
1
кр1
0 0
cos .
dx
d
Вычисление двойного интеграла приводит к следующей формуле:
2
кр1
1 .
H H
Чтобы найти весь средний угол,
следует провести аналогичные рас-
четы и для второго критического
угла θ
кр2
или, исходя из очевидной
симметрии задачи, умножить полу-
ченное выражение на 2.
Для определения вероятности
вылета частиц из системы без
столкновений со стенками необ-
ходимо учитывать нормирующий
множитель:
Общая схема щелевого канала


