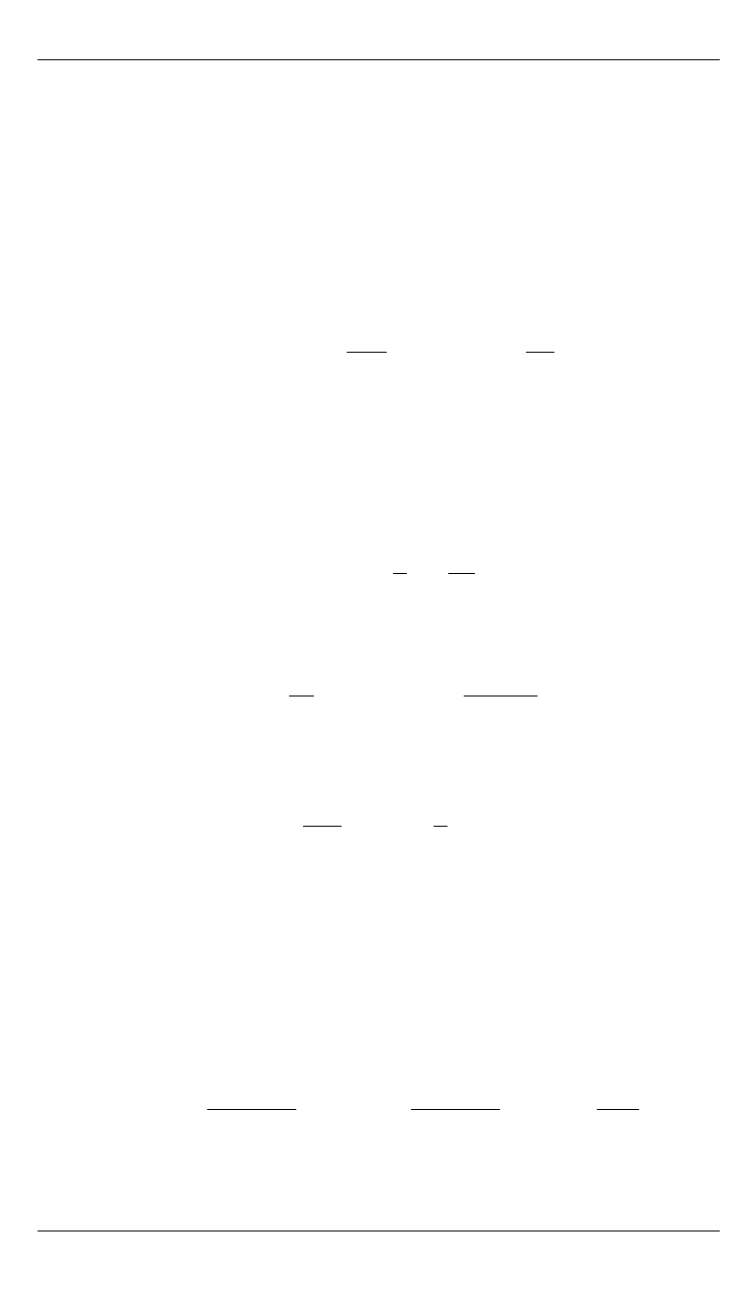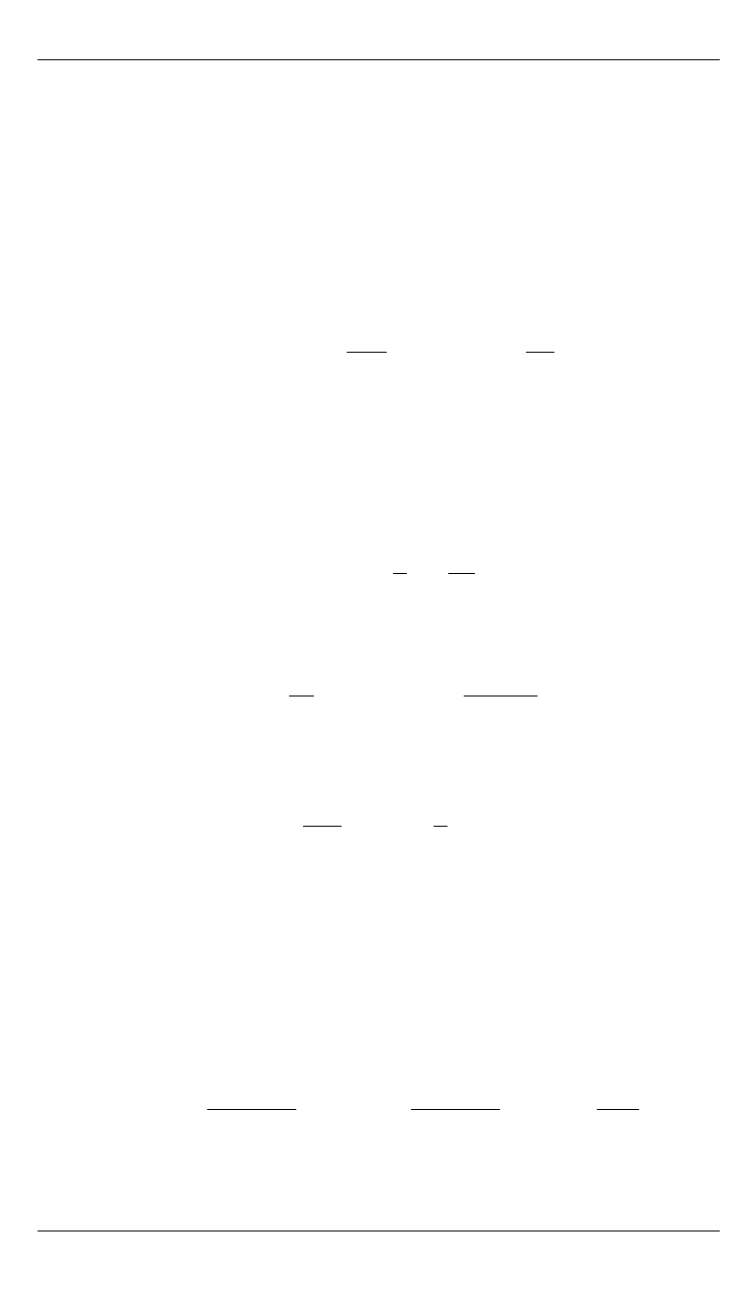
Ю.Ю. Инфимовский, М.А. Строков
4
зависимости от давления в канале и соотношения размер рабочей ка-
меры/длина пробега возмущения в воде за время разряда. В данной
работе использованы численные расчеты на основе модели расшире-
ния сферы в неограниченной несжимаемой жидкости [10] с поправ-
кой на унос энергии за счет акустических колебаний.
Для случая, когда давление в канале слишком мало и можно не
учитывать энергию сжатия воды, запишем уравнение баланса энер-
гии:
2
3
пл кин 0
0
0
1
2
,
1
dR
E E E p V
pV
R
p V
dt
(1)
где
пл кин
,
E E
– энергия плазмы и кинетическая энергия;
0
p
– атмо-
сферное давление;
V
– объем плазмы;
0
– начальная плотность во-
ды;
– показатель адиабаты плазмы;
R
– радиус плазменной поло-
сти;
р
– давление воды.
Из уравнения непрерывности
2
1
( ) const
2
h u
f t
t
(
grad ,
u
h
– энтальпия) при
0
const
после преобразований получаем
4 2
2 2
0
0
0
4
(
)
(2
)
.
2
R R
p r R
RR R R
p
r
r
(2)
При
r
=
R
выражение для ускорения поверхности сферы имеет вид
2
0
0
0
1
3
.
2
R
p p
R
R
(3)
Численно проинтегрировав выражение (3), получаем закон рас-
ширения сферы. Затем из соотношения (2) определим давление на
любом расстоянии от разряда в заданный момент времени.
Для того чтобы частично учесть сжимаемость воды и определить
уносимую за счет акустических волн энергию, введем в алгоритм
расчета поправку:
2
2
2
0
0
2
2
2
в 2
в в
в в
в в
4
2
2
,
2
p p
p p
p
dE R
c dt
R
dt
R dt
c
c
c
(4)
где
в
– плотность воды;
в
c
– скорость звука в воде.