К.Л. Тассов, Р.А. Дятлов
8
[ ]
[ ]
1
1 π
cos
, 1
2
P
n
n
k
C j
X k
j k
j J
P
=
⎛
⎞
⎛
⎞
=
−
≤ ≤
⎜
⎟
⎜
⎟
⎝
⎠
⎝
⎠
∑
,
(16)
где
C
n
[
j
] — массив кепстральных коэффициентов;
J
— желаемое чис-
ло коэффициентов (
J
<
P
).
Распознавание диктора.
На данном этапе обработки данных
происходит идентификация диктора по характеризующим признакам.
Для этого применяется модификация сети встречного распростране-
ния Кохонена — Гроссберга [4]. Слой Кохонена в описываемой мо-
дификации представляет собой самоорганизующуюся карту Кохоне-
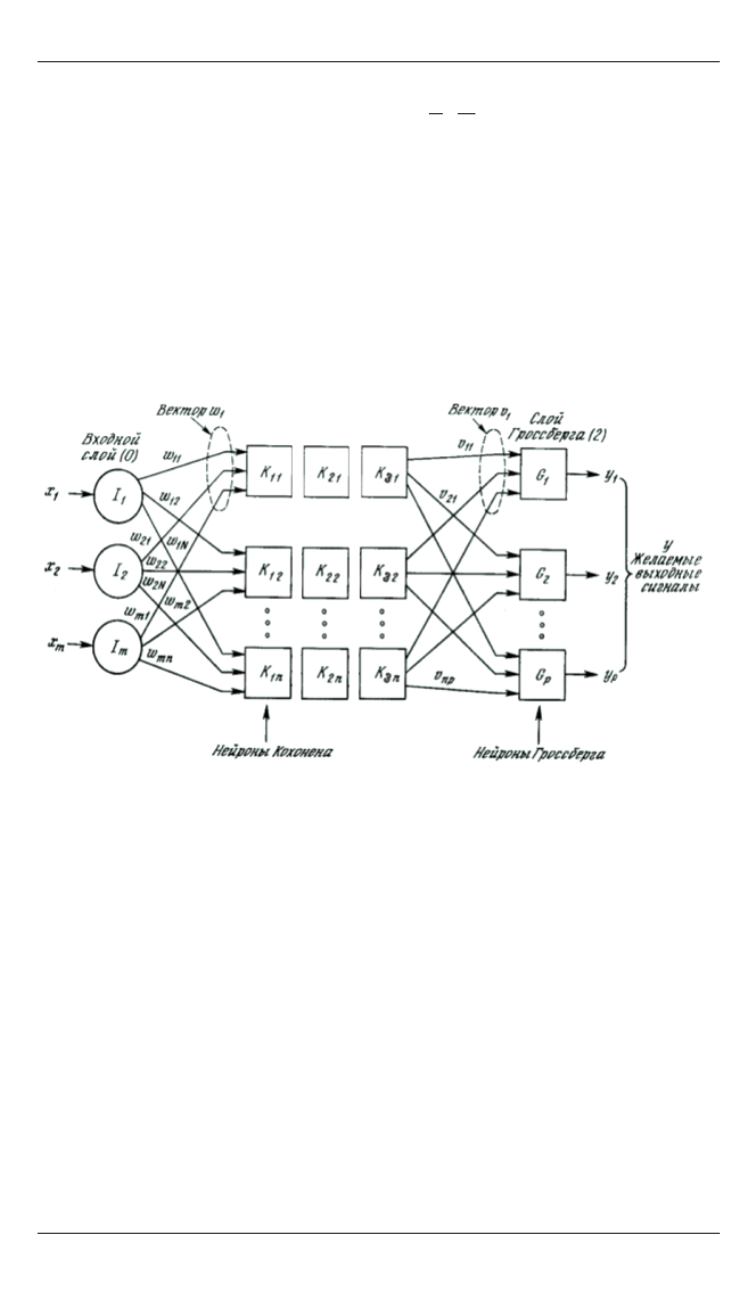
на [5, 6]. На рис. 9 представлена топология данной сети.
Рис. 9.
Модификация сети встречного распространения
Во встречном распространении объединены два хорошо известных
алгоритма: самоорганизующаяся сеть Кохонена и звезда Гроссберга.
В процессе обучения входные векторы ассоциируются с соответ-
ствующими выходными векторами. Они могут быть двоичными, со-
стоящими из нулей и единиц, или непрерывными. Когда сеть обуче-
на, приложение входного вектора приводит к требуемому выходному
вектору. Обобщающая способность сети позволяет получать пра-
вильный выход даже при приложении входного вектора, который яв-
ляется неполным или слегка неверным.
Самоорганизующиеся карты Кохонена представляют собой
нейронные сети, обучаемые без учителя. Они используются для клас-
сификации, организации и визуального представления больших объ-
емов данных. Важной особенностью карт Кохонена является их спо-
собность отображать многомерные пространства признаков на плос-


