В.Ф. Жирков, И.Д. Маслов
4
После очередного сдвига влево на одну двоичную позицию дво-
ичные числа в тетрадах, значения которых до сдвига не превышали
4
10
= 0100
2
, удваиваются (умножаются на 2), так как цифра в тетраде
с весом 4 приобретает вес 8, с весом 2 — вес 4, с весом 1 — вес 2.
Однако после сдвига могут возникнуть псевдотетрады, если до
сдвига тетрады имели значения 5, 6, 7. Псевдотетрады корректируют
после каждого сдвига, прибавляя к ним 6
10
= 0110
2
с передачей еди-
ницы переноса в соседнюю старшую тетраду.
Те тетрады, которые имели до сдвига значения 8 или 9, также
необходимо корректировать. Из таких тетрад при сдвиге влево про-
исходит передача единицы в соседнюю старшую тетраду. Поскольку
разрядное значение этой единицы при сдвиге увеличивается с 8 до
16, а в соседней старшей тетраде она приобретает вес 10, то двоично-
десятичное число уменьшается на 6 единиц той тетрады, из которой
произошла передача единицы. Таким образом, и в этом случае кор-
рекция состоит в прибавлении 6
10
= 0110
2
к этим тетрадам.
Однако коррекцию целесообразно проводить не после сдвига
прибавлением 6
10
, а до сдвига прибавлением 3
10
= 0011
(2)
к тем тетра-
дам, которые имеют значения от 5 до 9 включительно. При такой
коррекции после сдвига не возникают псевдотетрады и образуется
правильное произведение.
Элементарный преобразователь (ЭП) двоичного кода в дво-
ично-десятичный код, реализующий коррекцию.
ЭП должен вы-
полнять функцию
, если 0
4,
3, если 5
9,
X
X
Y
X
X
(5)
где
4 3 2 1
4 3 2 1
(
) и (
)
X x x x x Y y y y y
— двоичные числа на входе и
выходе ЭП;
х
4
,
y
4
— старшие разряды.
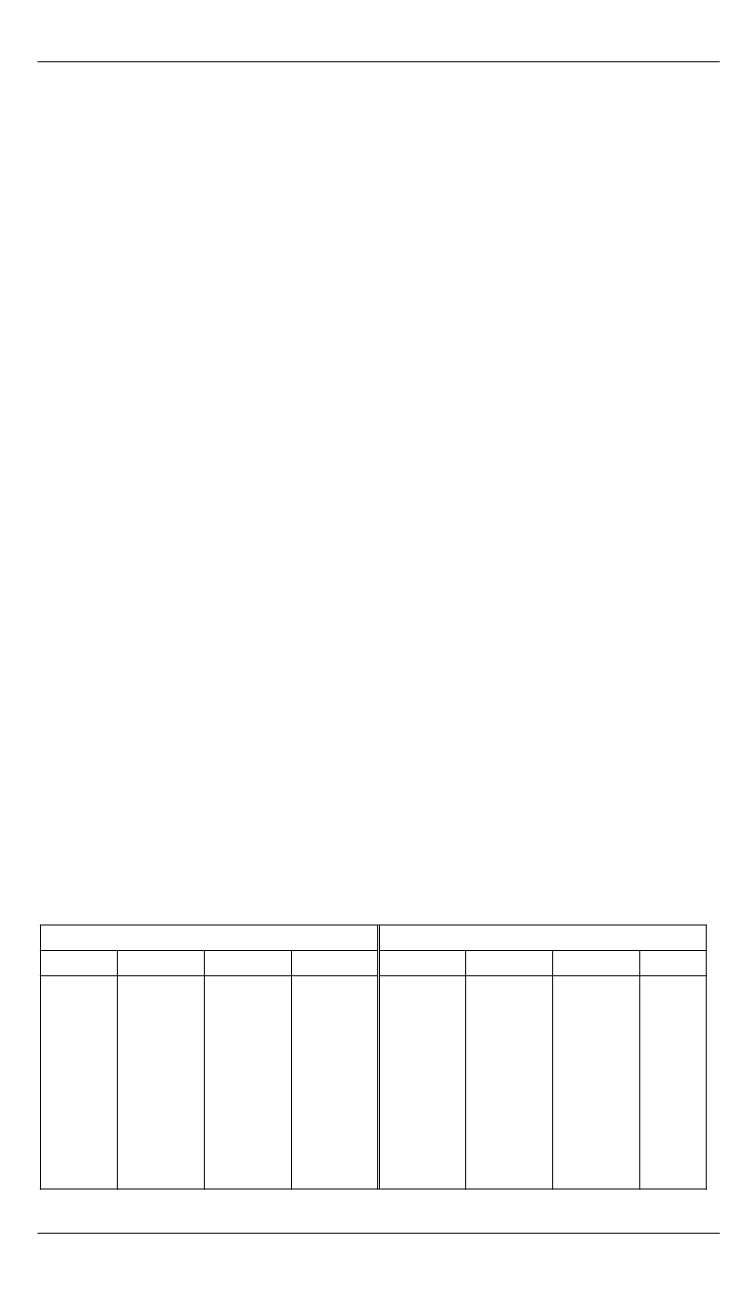
Работа ЭП поясняется приводимой ниже таблицей истинности.
Таблица истинности ЭП
Входы
Выходы
x
4
x
3
x
2
x
1
y
4
y
3
y
2
y
1
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
1
1
1
0
0
0
0
1
1
0
0
1
1
0
0
0
1
0
1
0
1
0
1
0
1
0
0
0
0
0
0
0
0
1
1
0
0
0
0
1
1
1
1
0
0
0
0
1
1
0
0
1
1
0
0
0
1
0
1
0
1
0
1
0
1


