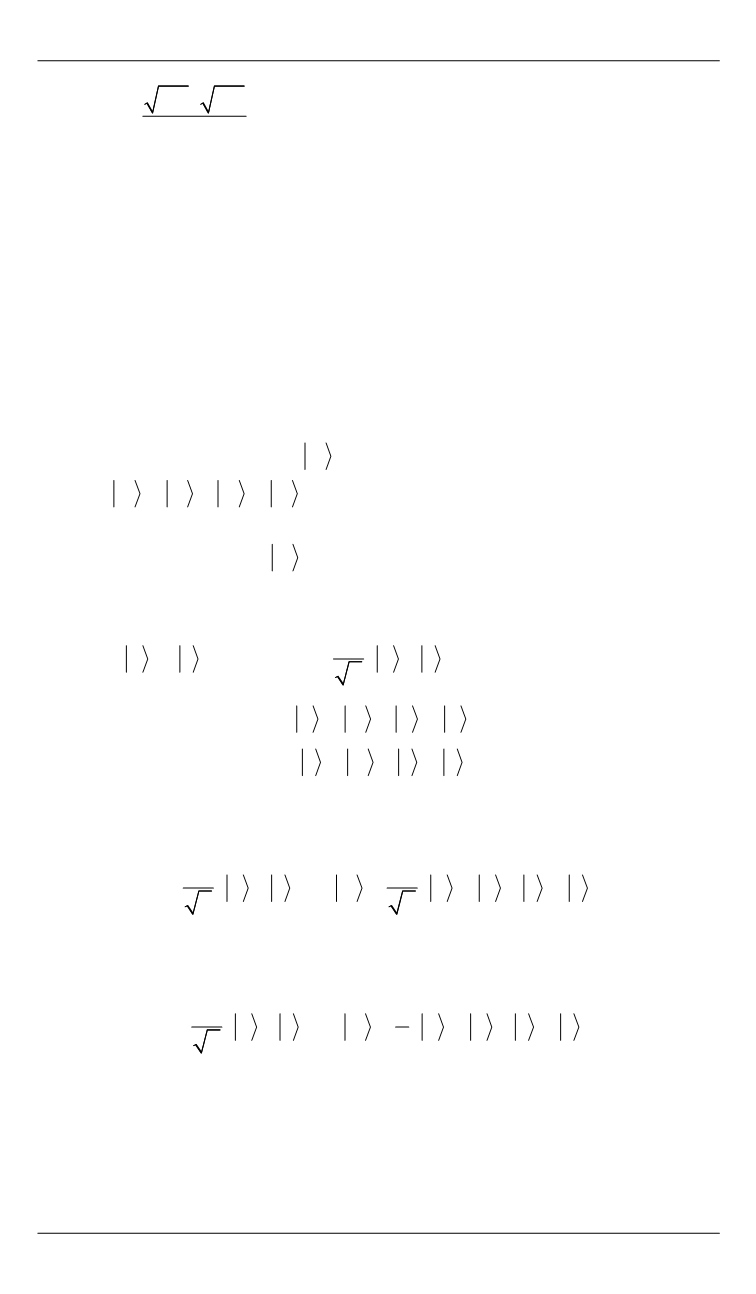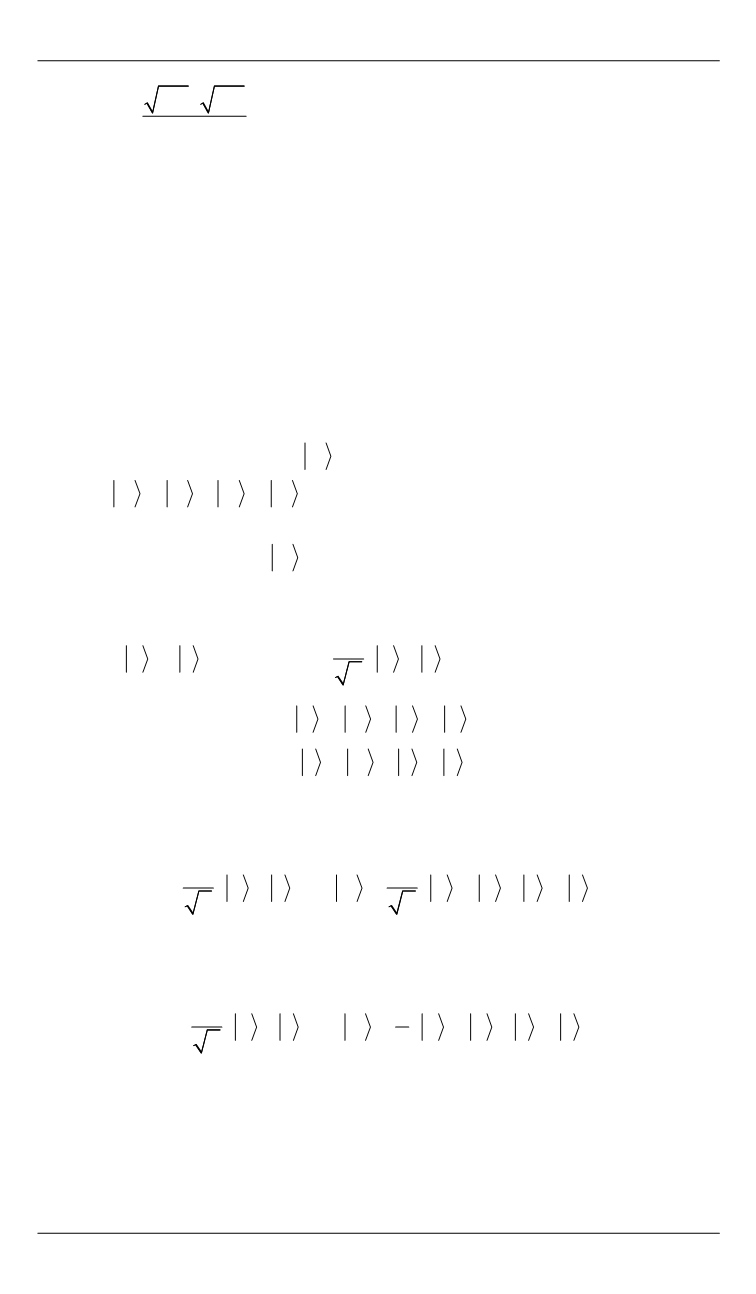
Е.Ю. Иванова, Е.А. Ларионцева
4
но в
.
Tr
i
i
i
i
M M
M
Данное утверждение свидетельствует о том,
что попытки измерить состояние системы ведут к помехам в ней, а
значит, к возникновению ошибок на стороне приемника, которые
можно легко обнаружить. Это поведение системы очень удобно и
важно в криптографии.
Неортогональные квантовые состояния обладают еще одним
важным свойством —
невозможностью (запретом) их клонирования
.
Потребность в клонировании состояний может возникнуть, напри-
мер, у злоумышленника, пытающегося собрать полную статистику
результатов измерений.
Приведем пример, показывающий невозможность клонирования
состояний. Под преобразованием
U
, клонирующим некоторое чи-
стое квантовое состояние
,
понимается следующее преобразова-
ние:
U A
(как было показано ранее, любое преоб-
разование квантовой системы можно описать унитарным операто-
ром). В этой формуле
A
— исходное состояние вспомогательной
системы.
Рассмотрим действие данного преобразования на квантовые со-
стояния
0
и
1
и состояние
1 0 1 :
2
0
0 0 ,
U A
(1)
1
1 1 .
U A
(2)
Так как оператор
U
линейный, то на основании формул (1) и (2)
получаем
1
1
0 1
0 0 1 1 .
2
2
U
A
C другой стороны, согласно определению
U
имеет место соотно-
шение
1
1
0 1
0 0 1 1 .
2
2
U
A
Получаем противоречие, значит, первоначальное предположение
о возможности клонирования неортогональных состояний ошибочно.
Квантовый протокол BB84.
Идея использования квантовых
объектов для защиты информации от подделки и несанкционирован-
ного доступа впервые была высказана Стефаном Вейснером в 1970 г.