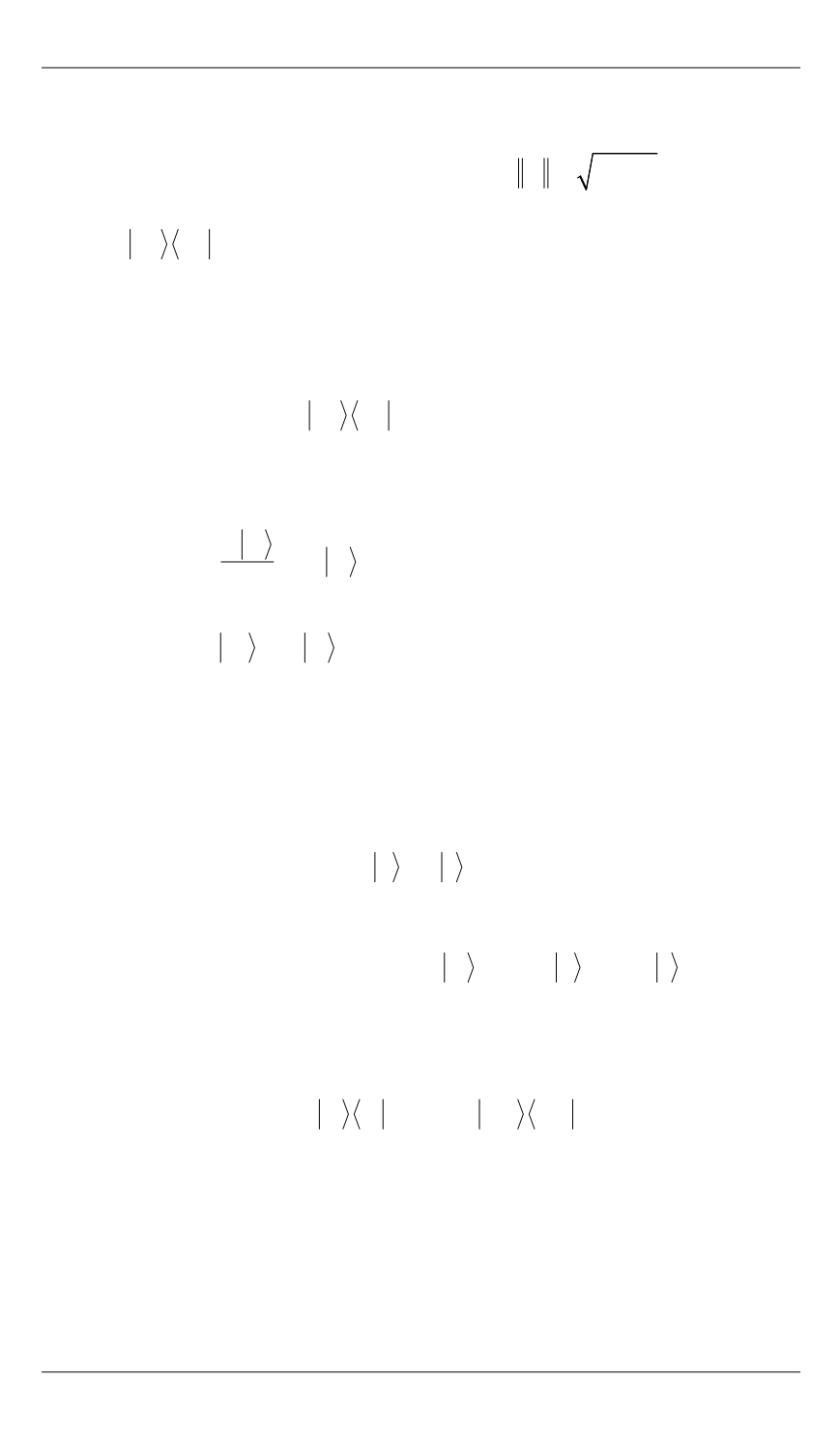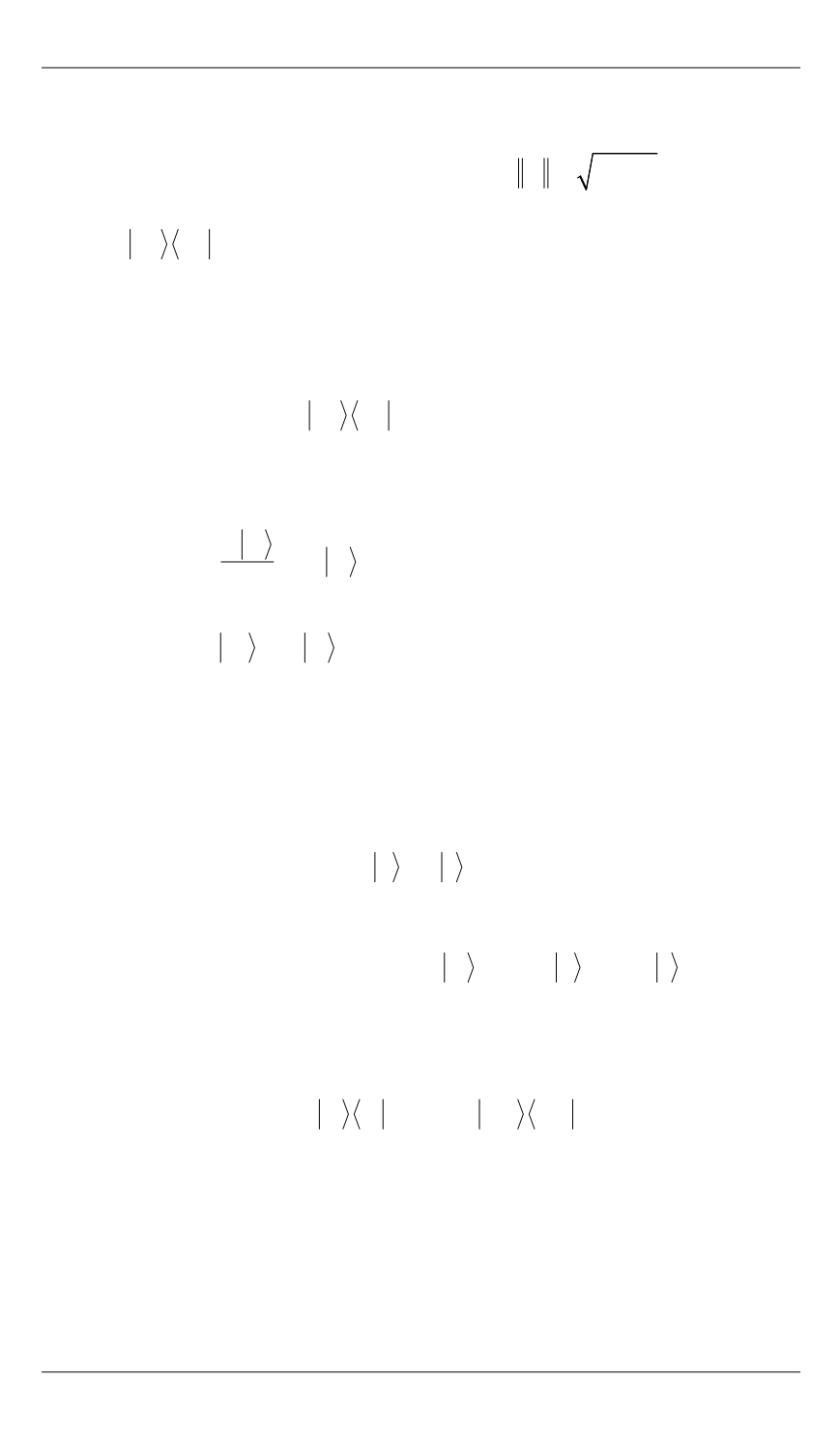
Введение в квантовую криптографию: основные понятия, подходы и алгоритмы
3
Квантовые состояния подразделяют на два вида: чистые и смешан-
ные.
Чистым квантовым состоянием
называют вектор в
гильбертовом
пространстве
H
c единичной нормой, т. е.
.
, ,
H
=
Для
каждого чистого квантового состояния определен оператор плотно-
сти
,
i
i
имеющий единичный след и ранг, равный 1. Данный
оператор действует как проектор на чистое квантовое состояние.
В свою очередь,
смешанное квантовое состояние —
это стати-
стическая смесь нескольких чистых состояний, т. е. чистых состоя-
ний с соответствующими вероятностями:
,
0 ,
1.
i
i
i
i
i
i
i
p
p
i
p
Ключевым аспектом в квантовой теории информации является
теорема Шредингера. В классическом виде она может быть сформу-
лирована как
.
d
i
H
dt
Однако в силу соответствия между эр-
митовым и унитарным оператором
iH
U e
теорема принимает сле-
дующий вид:
.
U
Данное представление демонстрирует
важное свойство квантовых систем, которое используется при по-
строении квантовых каналов передачи информации, а именно: любое
изменение в системе может быть описано унитарным оператором.
Примером квантового объекта могут быть системы, состоящие из
двух базисных состояний. Тогда гильбертово пространство имеет
размерность 2 и обозначается
2
.
H
Примером такой системы может
быть система с состояниями
0
и
1
в качестве базисных. Данная
система носит название «
кубит
» (квантовый бит).
Любое состояние кубита в произвольный момент времени может
быть записано следующим образом:
cos 0 sin 1 .
Ранг оператора плотности
равен 1 для чистых квантовых со-
стояний и 2 для смешанных, которые могут быть представлены как
статистическая смесь двух ортогональных состояний:
1
.
p
p
Следует непременно рассмотреть такое явление, как коллапс
волновой функции
.
Под
коллапсом волновой функции
(или
редукци-
ей фон Неймана
)
понимается мгновенное изменение волновой
функции объекта, происходящее при его измерении. Пусть
i
M
—
текущее измерение,
i —
полученный результат. Отсюда исходное
состояние в результате проведенного измерения будет преобразова-