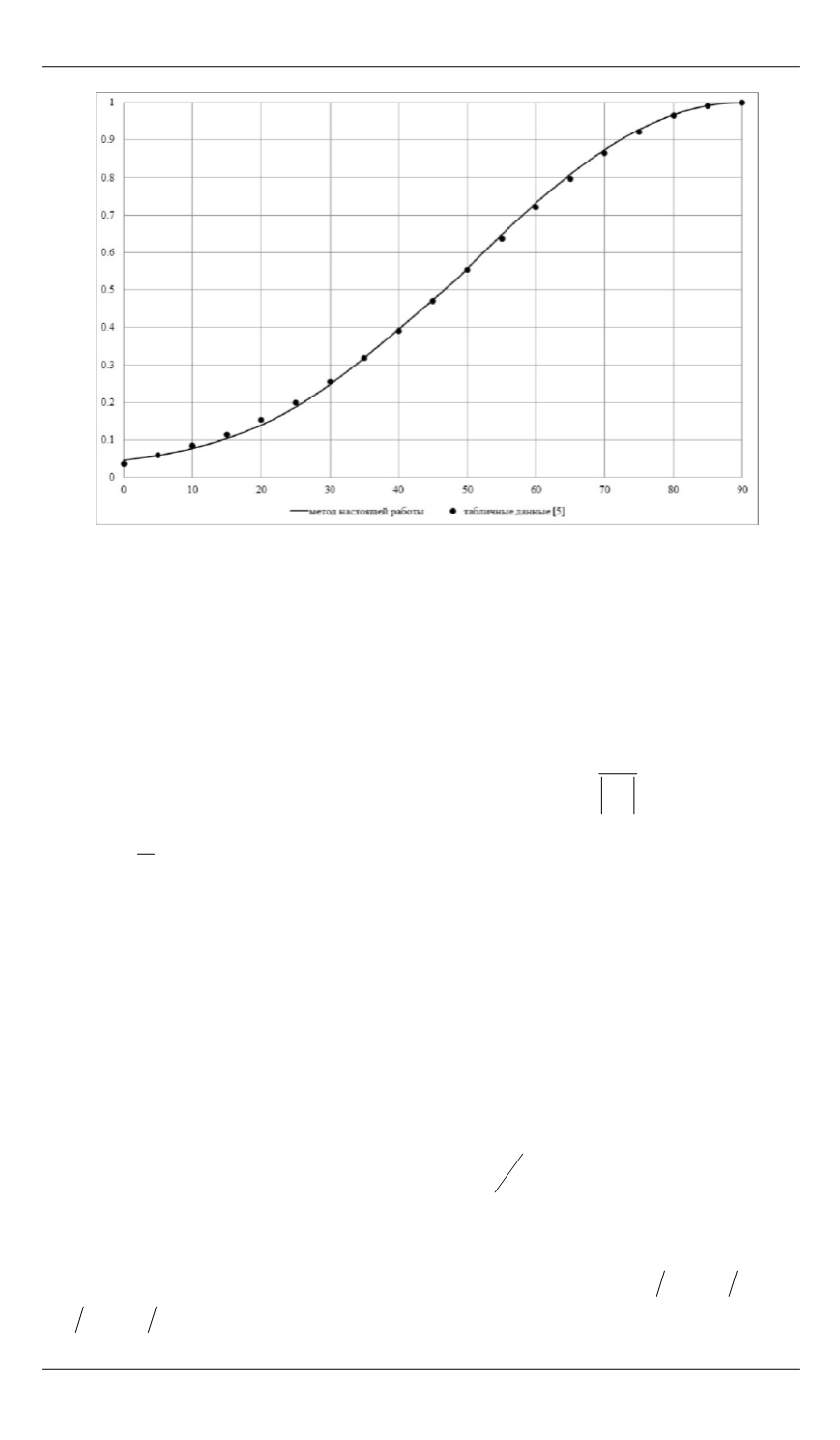
Применение правила местных сфер для расчета давления на затупленных телах
5
Рис. 2.
Сфера, М = 6
Далее вычислим распределение давления на поверхности эллипсо-
ида. Такой выбор обусловлен наличием данных для задачи о стацио-
нарном пространственном обтекании сверхзвуковым потоком идеаль-
ного газа головной части затупленного тела, полученных методом
установления в работе [6]. В соответствии с правилом местных сфер
давление на эллипсоиде в точке, где угол arccos
,
V n
V
совпадает
с углом
2
на сфере, полагалось равным давлению на сфере с дан-
ным углом встречи потока с поверхностью. Здесь
n
– единичная нор-
маль на эллипсоиде в текущей расчетной точке. Рассматривались слу-
чаи, когда вектор набегающего потока образует с осью эллипсоида
a
угол
10
и параллелен плоскости, которая проходит через ось
a
и
составляет с осью
b
угол
0, 30, 60, 90 .
Угол сферической системы
координат
изменялся от
0
до
90
(рис. 3).
Влияние угла
на распределение безразмерного давления (дав-
ление отнесено к удвоенному скоростному напору) по поверхности
эллипсоида с отношением полуосей
2 1: 1: 3 в различных плоскостях
const
при M 3
, приведено на рис. 4–7. Полюс системы коор-
динат при этом располагается в центре эллипсоида. Цифрами
1
,
2
,
3
,
4
,
5
,
6
обозначены меридиональные плоскости
0,
3,
2 3,
,
4 3,
5 3
. Сплошной линией на рисунках обозначены результаты


