В.П. Котенев, А.Ю. Дубровина
4
где
*
*
*
*
1
;
( ) ( )
( )
f
r
P V P
0
0
0
0
1
( )
( )
( )
f
r
P V P
, здесь
0
P
вычисляем по формуле
2
0
0
*
2
*
sin
sin
P
P P
P
.
Основываясь на [2], получим уравнение зависимости
P
на от-
резке
0
5 ,
18
:
1
1
2
* 0
0
0
2
* 0
1
1
.
2
P P
f
f
r
f
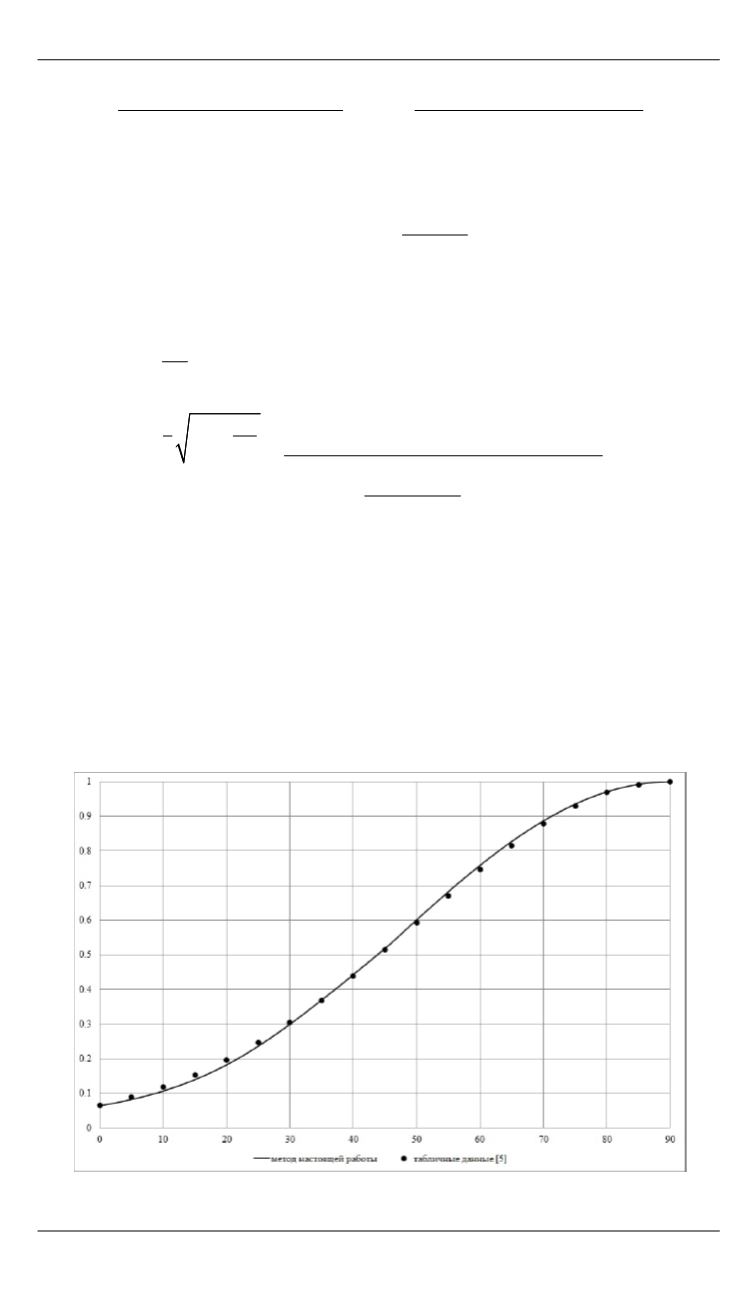
Анализ результатов.
Для начала сравним табличные данные
распределения давления на поверхности сферы, приведенные в [5],
с результатами расчета. Из рис. 1 и 2 видно, что расчетные данные
хорошо согласуются с табличными, что позволяет сделать предполо-
жение о возможности использования полученных ранее формул для
нахождения распределения давления на поверхности затупленных
тел.
Рис. 1.
Сфера, М = 3


