3
Перспективы получения нанометровойшероховатости поверхности ионно-лучевымметодом
Y
р
(
)
= Y
p
(0)
/ cos
,
где
Y
p
(0) — коэффициент распыления
при нормальном падении ионов.
Данная зависимость основана на
механизме физического распыления.
Коэффициент распыления при нор-
мальном падении ионов прямо про-
порционален энергии, рассеиваемой в
поверхностном слое материала, в пре-
делах которого упругие столкновения
будут приводить к распылению. При
угле падения
длина пробега ионов, а
следовательно, и число столкновений
в этом слое будут в 1/cos
раз больше.
Форма микронеровностей шерохо-
ватой поверхности после механической
обработки моделируется различными
геометрическими фигурами: пирамида-
ми, полусферами, конусами и др. Пира-
мида является одной из наиболее рас-
пространенных моделей микронеров-
ности поверхности детали после шли-
фования (рис. 2), поэтому расчет зави-
симости коэффициента распыления
материала
Y
p
от угла падения
ведется
для микронеровности в виде пирамиды
с углом при вершине
.
Расчет коэффициента распыления
Y
p
в зависимости от угла падения ион-
ного пучка φ в диапазоне от 0 до 85°
(угол
более 60° использован в спра-
вочных целях) и угла при вершине пи-
рамиды
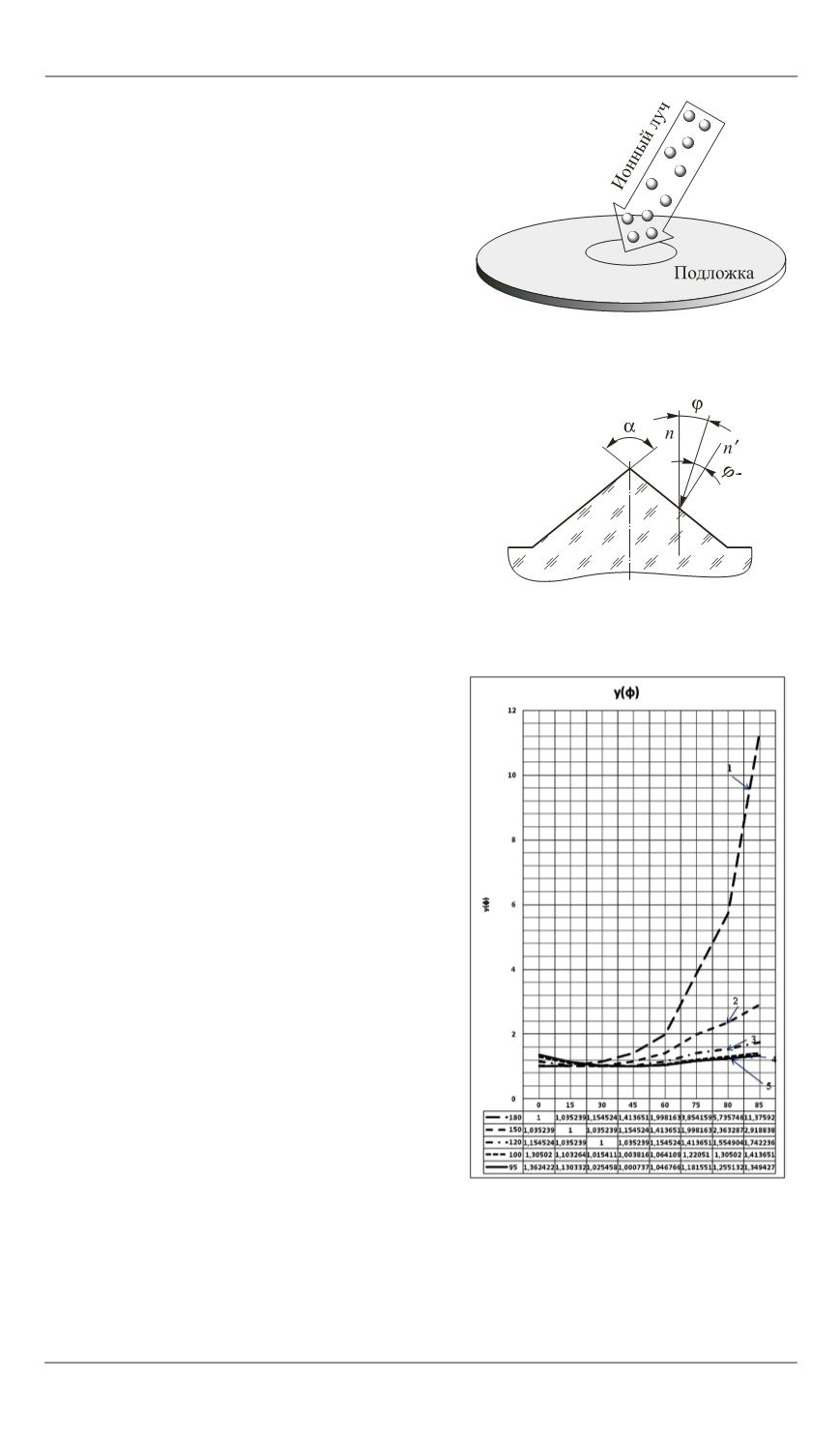
в диапазоне от 180 до 95°
показал неожиданный для нас резуль-
тат: коэффициент распыления матери-
ала, а следовательно, скорость ионного
травления, мало зависят от угла
,
если угол падения ионного пучка
ра-
вен 20° (рис. 3).
Чтобы объяснить полученные
результаты расчета, были построены
пять геометрических моделей с углом
Рис. 3.
Зависимость коэффици-
ента распыления
Y
p
от угла паде-
ния ионного пучка
от 0 до 85°
и угла при вершине пирамиды α:
1
— 180°;
2
— 150°;
3
— 120°;
4
— 100°;
5
— 95°
Рис. 1.
Модель ионного бомбарди-
рования поверхности подложки
Рис. 2.
Модель микронеровности
поверхности в виде пирамиды


