Исследование режимов плавки для удаления гололедных образований на грозозащитных…
7
Как видно из формулы (3), толщина нагрева будет еще больше.
Таким образом, в математической модели принимается, что время
нагрева ледяной муфты равно нулю, т. е. его можно не учитывать.
Мощность, выделяемая вследствие прохождения электрического то-
ка, расходуется на нагрев ОКГТ, плавку и нагрев ледяной муфты, а
также на компенсацию потерь теплоты за счет излучения и конвек-
цией с поверхности льда.
Необходимо отметить следующее: в случае изморози время
нагрева может быть значительным, так как ее теплопроводность
очень мала — 0,05…0,2 Вт/(м
⋅
°С). Однако при этом погрешность
расчета практически не увеличивается, поскольку потери теплоты за
счет конвекции и излучения малы по сравнению с теплотой, расходу-
емой на плавку льда и нагрев ОКГТ.
Вывод аналитической формулы.
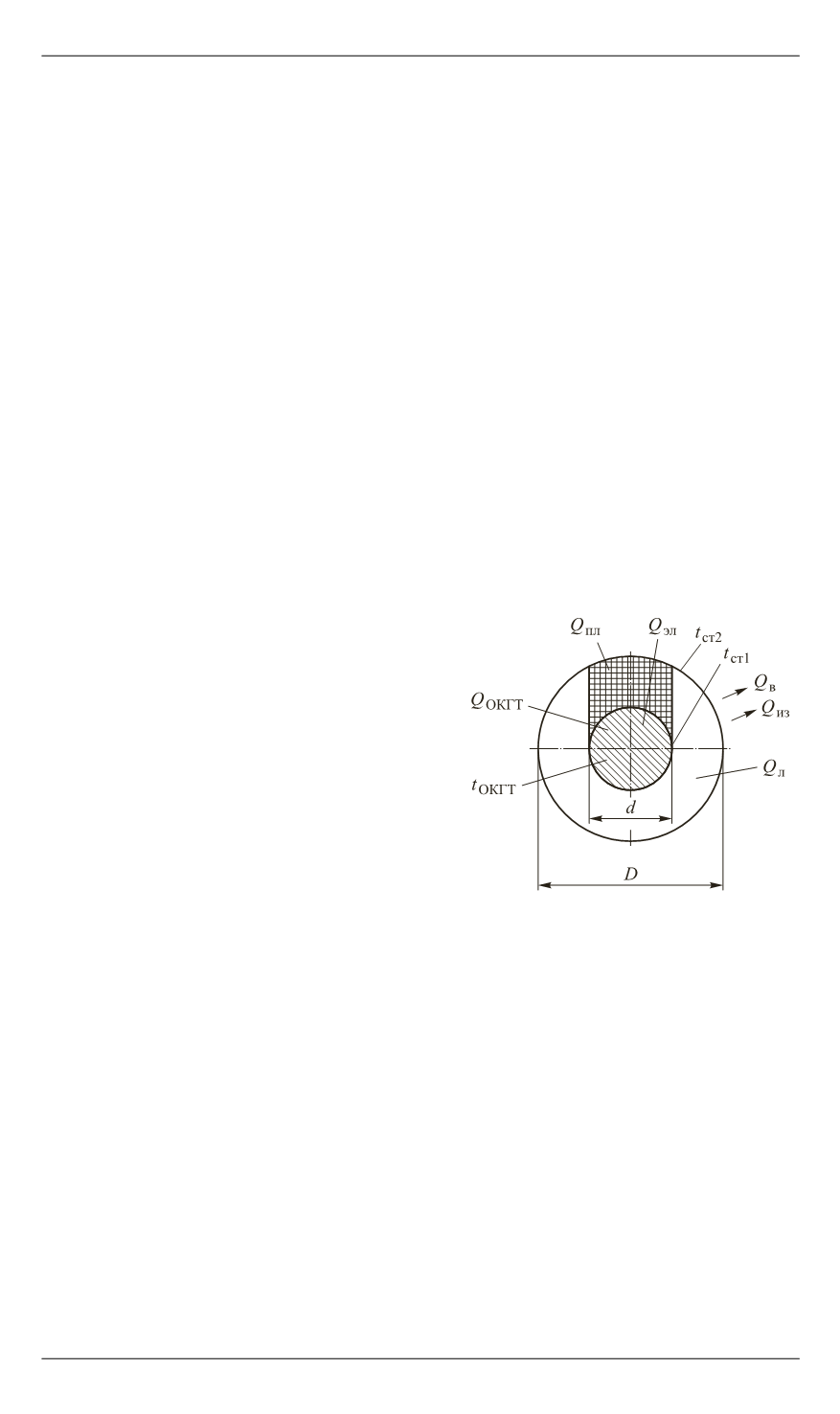
Тепловой баланс (рис. 4)
определяется следующим уравнением (рассматривается количество
теплоты на 1 м ОКГТ):
Q
эл
+
Q
сол
=
Q
пр
+
Q
л
+
Q
пл
+
Q
в
+
Q
из
,
где
Q
эл
— теплота, выделяемая
вследствие прохождения электриче-
ского тока по ОКГТ (подводимая
теплота), Дж/м;
Q
сол
— теплота, под-
водимая за счет солнечного излуче-
ния, Дж/м;
Q
пр
— теплота, затрачива-
емая на нагрев провода, Дж/м;
Q
л
—
теплота, затрачиваемая на нагрев
льда, Дж/м;
Q
пл
— теплота, затрачи-
ваемая на плавку льда, Дж/м;
Q
в
—
теплота, отводимая за счет конвек-
ции в воздухе, Дж/м;
Q
из
— теплота,
отводимая за счет излучения, Дж/м.
При этом
Q
эл
=
I
2
R
эл
Δτ
,
где
I
— ток плавки, А;
R
эл
— удельное электрическое сопротивление
ОКГТ, Ом/м;
Δτ
— время плавки, с.
Теплота, подводимая за счет солнечного излучения, принимается
равной нулю.
Теплота, затрачиваемая на нагрев,
(
)
ОКГТ ОКГТ в
1
,
n
i i i
i
Q t
t
С S
=
=
−
ρ
∑
Рис. 4.
Схема к выводу аналити-
ческой формулы


