
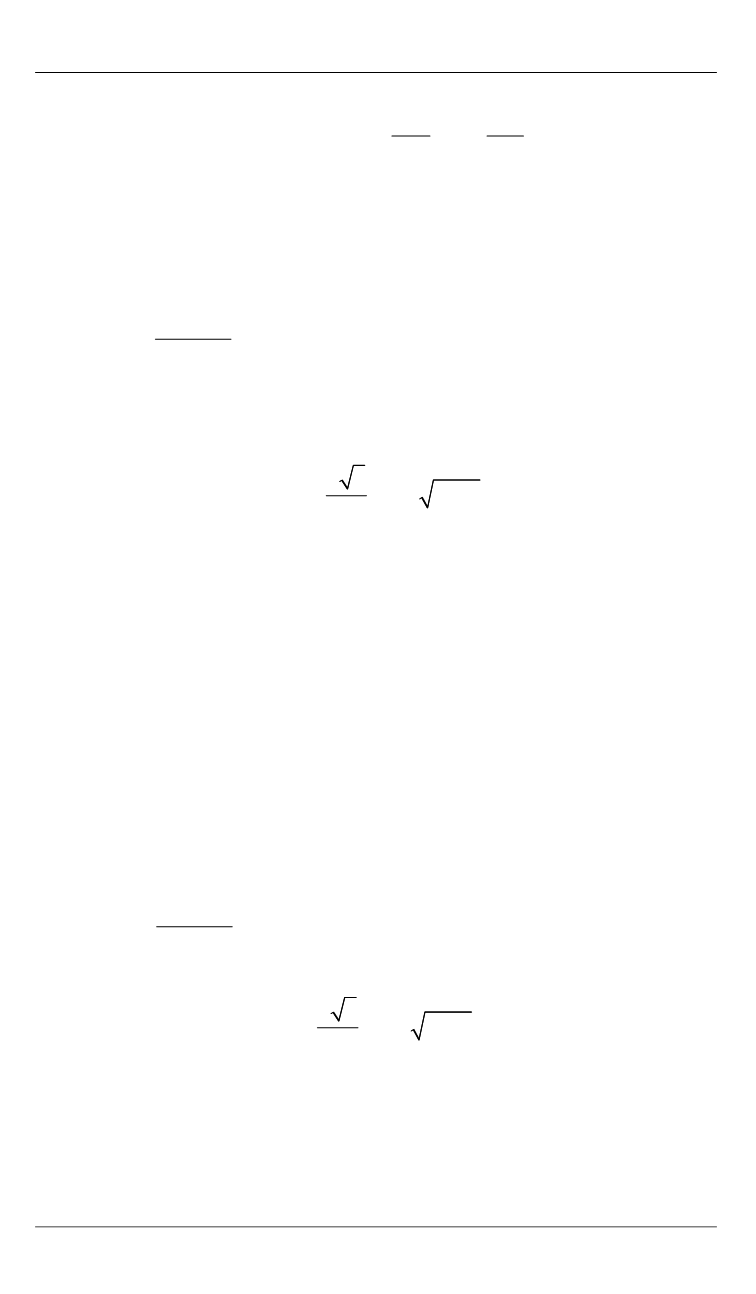
Проектирование вафельных оболочек топливных баков ракеты…
Инженерный журнал: наука и инновации
# 11·2017 3
В выражение (3) введены в дальнейшем варьируемые безразмер-
ные геометрические параметры
исх
2 ,
.
π
ψ =
ϕ =
h
c
h
b
Погонная жесткость растяжения — сжатия продольного сечения
подкрепленной оболочки:
2
2
,
=
B Eh
(4)
где
2
2
=
h hH
— приведенная толщина продольного сечения оболоч-
ки,
2
( 1)
1
.
2
ψ − ϕ
= +
π
H
Подставив в формулу (1) выражения для (2) и (4), получим кри-
тическую осевую нагрузку подкрепленной оболочки (идеальной обо-
лочки)
2
кр
2
2 3
.
3
= π
N
Еh HH
Как известно, критическая осевая нагрузка подкрепленной обо-
лочки зависит от начальных несовершенств, внутреннего давления —
давления наддува [5], а в том случае, когда материал оболочки при
потере устойчивости находится за пределами упругости, то и от его
соответствующих механических характеристик. Для их учета введем
понятие гладкой эквивалентной оболочки [6], равной массе рассмат-
риваемой подкрепленной оболочки. Из равенства объемов таких обо-
лочек можно определить толщину эквивалентной оболочки
э
.
h
Пред-
полагается, что влияние перечисленных факторов на устойчивость
подкрепленной оболочки [7] такое же, как на гладкую эквивалентную
оболочку толщиной
э
:
h
э
3
,
=
h hH
(5)
где
3
( 1)
1
.
2
ψ − ϕ
= +
π
H
Тогда для подкрепленной оболочки
2
кр
э
2
2 3
.
3
= π
N
Еh HH
(6)
Точно так же можно определить погонную жесткость на растя-
жение — сжатие поперечного сечения подкрепленной оболочки
1
1
.
=
B Eh
(7)
Здесь
1
1
=
h hH
— приведенная толщина поперечного сечения обо-
лочки, коэффициент
















