Моделирование ударно-волновых процессов в элементах многослойных конструкций с учетом начального внутреннего давления

4 / 10

Т.А. Бутина, В.М. Дубровин
4 Инженерный журнал: наука и инновации # 11·2016
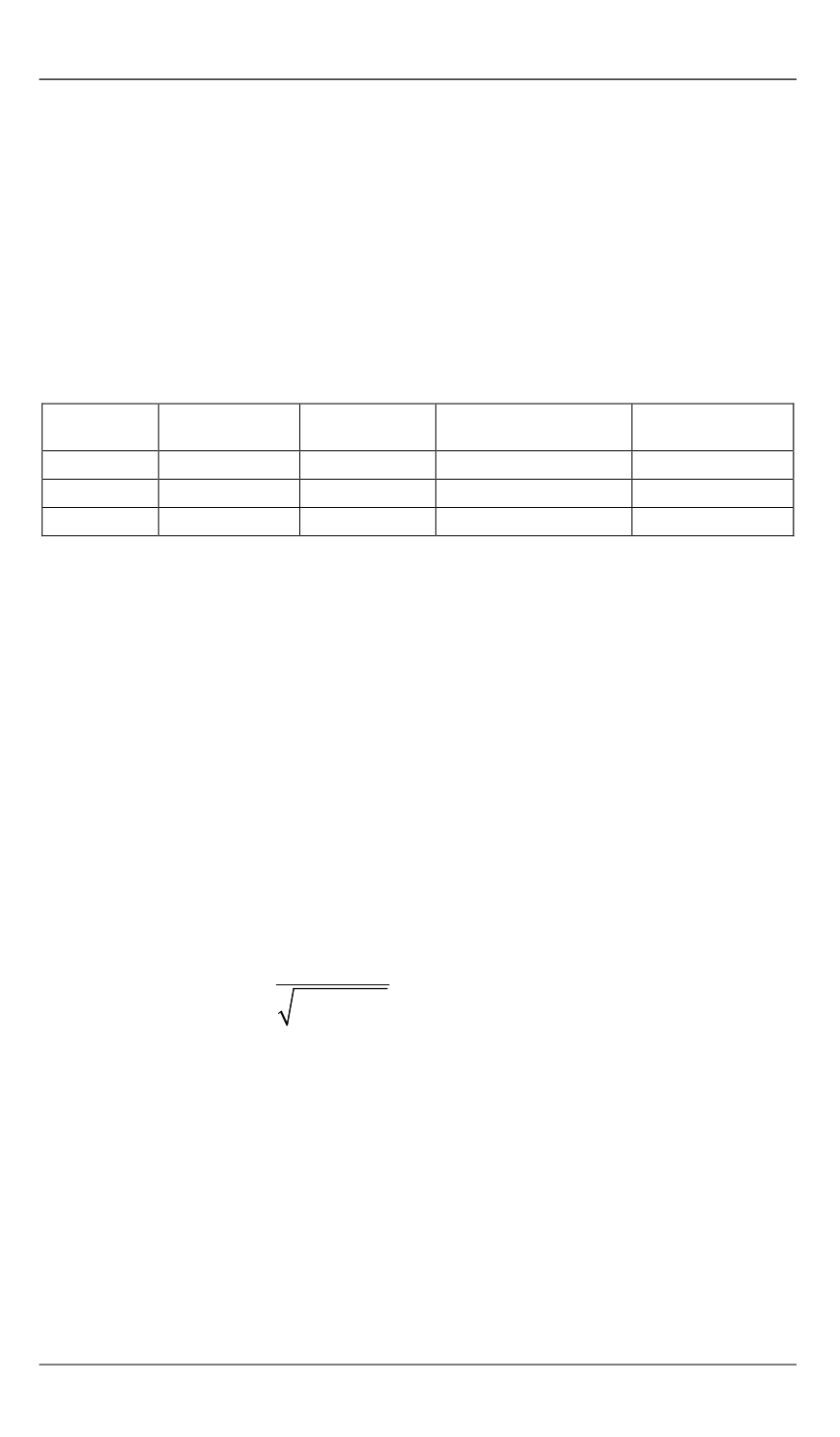
В качестве уравнения состояния рассматривалось уравнение со-
стояния Ми — Грюнайзена
y 0 y γ ( ), P P E E= ( − (5)
где y у, P Е — упругие составляющие давления и энергии.
Результаты расчетов. Расчеты проводили на примере трехслой-
ной цилиндрической оболочки, основные характеристики которой
приведены в таблице. Внешний радиус оболочки 120 см.
Основные характеристики трехслойной цилиндрической оболочки
Номер слоя Толщина h,
см
Плотность
ρ, г/см3
Объемный модуль
K , Па
Модуль сдвига
G, Па
1 1,2 1,35 3,7 ⋅109 1,7 ⋅ 108
2 0,18 1,08 2,4 ⋅109 2,5 ⋅ 108
3 1,2 1,8 5,2 ⋅109 5,4 ⋅ 108
Второй и третий слои принимали линейно-упругими, для матери-
ала первого слоя задавались различные значения предела текучести,
начиная от s σ =1 120 ⋅ 105 Па и выше. Внутреннее давление р о прини-
мали равным 10 ⋅ 105, 20 ⋅ 105 и 40 ⋅ 105 Па . Полученные расчетным
путем значения тангенциальных статических напряжений ст
θ σ в пер-
вом слое при чисто упругом поведении материала составили 710 ⋅ 105,
1 420 ⋅ 105 и 2 840 ⋅ 105 Па соответственно. Поскольку радиальные
статические напряжения ст
r σ на два порядка меньше, переход в пла-
стическую область при статическом нагружении определяется значе-
нием ст
θ σ .
В условиях плоской деформации (осевая деформация 0)
t ε =
ст
2
1,125 при 0,3.
1
s
s θ
σ
σ = ≈ σ γ =
− γ − γ
(6)
При действии динамической нагрузки на начальной стадии вол-
нового процесса преобладающими становятся радиальные напряже-
ния .
r σ
Динамическая нагрузка P(t) принималась прямоугольной формы,
5
max 1 10 Р = ⋅ Па, длительность 7
н 5 10 с. t −
= ⋅
На рис. 1 для трех приведенных значений внутреннего давления
приведены максимальные значения радиального напряжения r σ в пер-
вом слое в зависимости от прохождения волны напряжений по толщине
слоя, по оси абсцисс отложено число элементов; общее число двойных