
Оценка коэффициентов готовности орбитальной группировки
Инженерный журнал: наука и инновации
# 3·2016 5
Оценка коэффициента готовности
ОГ в случае восполнения.
Коэффици-
ент готовности ОГ, состоящей из
n
КА,
удобно рассчитать, используя метод
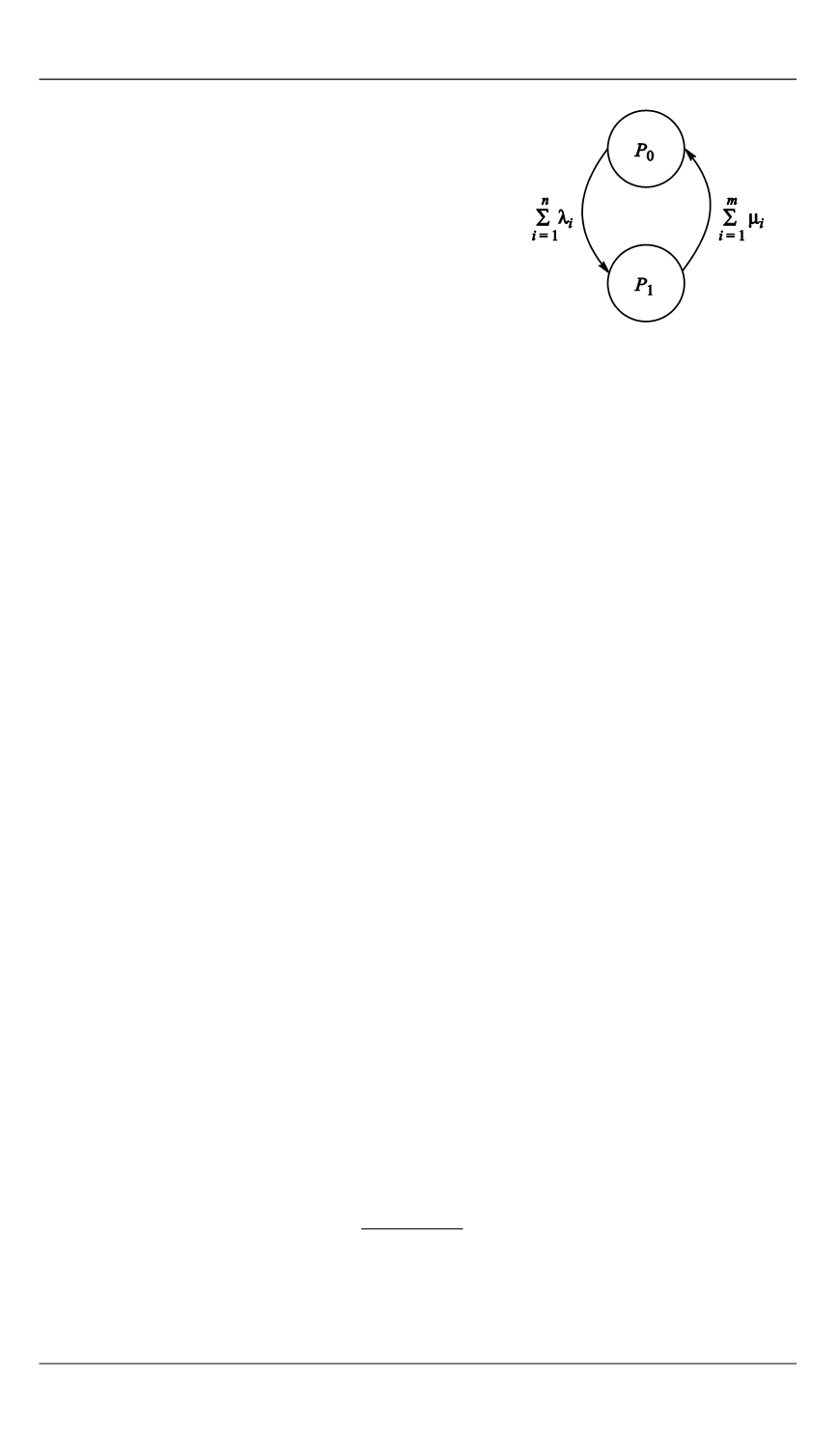
Маркова (ГОСТ Р51901.15–2015). На ри-
сунке представлена марковская модель
ОГ с учетом следующих условий:
•
существует всего два состояния
ОГ — работоспособное
0
( )
P
и нерабо-
тоспособное
1
( )
P
;
•
отказ одного КА из состава ОГ приводит к отказу ОГ;
•
все КА из состава ОГ имеют одинаковую интенсивность
отказов;
•
вероятность отказа НКУ не учитывать, так как время восста-
новления работоспособного состояния ОГ в случае отказа НКУ
пренебрежимо мало по сравнению со случаем отказа КА из состава ОГ.
На основании марковской модели ОГ (см. рисунок) можно постро-
ить математическую модель для расчета коэффициента готовности ОГ:
0
1
1
1
1
0
1
1
0 1
0;
0;
0,
n
m
i
i
i
i
m
n
i
i
i
i
P
P
P
P
P P
=
=
=
=
i − µ =
µ − i =
+ =
∑ ∑
∑ ∑
(9)
где
0
P
— вероятность того, что ОГ окажется работоспособной в про-
извольный момент времени
ОГ
(
);
K
0
P
— вероятность того, что ОГ
окажется неработоспособной в произвольный момент времени;
i
i
—
интенсивность отказов
i
-го КА из состава ОГ;
i
µ
— интенсивность
восстановления ОГ
i
-м числом КА;
m
— число КА, вводимых одно-
временно в состав ОГ для возобновления ее работоспособности;
n
—
число КА в составе ОГ.
Интенсивность восполнения ОГ
i
µ
определяется в соответствии
с формулами (6) и (8).
Интенсивность отказов
i
-го КА из состава ОГ можно рассчитать
по формуле
КА
АС
ln(
) ,
i
i
i
P
T
− i =
(10)
где
КА
i
P
— вероятность безотказной работы за САС
i
-го КА из со-
става ОГ;
АС
i
T
— САС
i
-го КА из состава ОГ.
Марковская модель ОГ


















