6
А.А. Гурченков, Е.К. Егорова
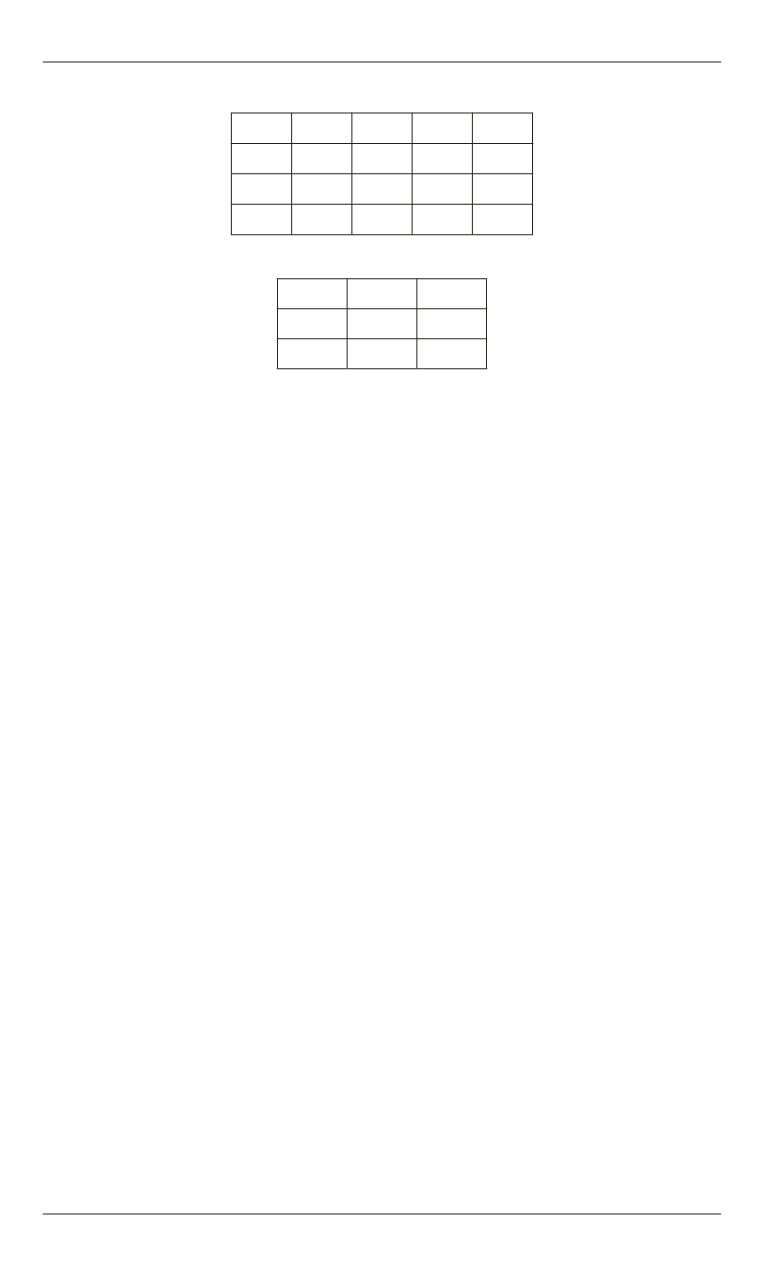
Таблица 5
x
2
x
3
x
4
p
K
1
1 1 0 2
K
2
0 0 1 1
r
1 1 1 3
Таблица 6
x
5
p
K
3
1
1
r
1
1
Следовательно, необходимо увеличить счетчик чтения
t
2
=
t
2
+ 1.
Таким образом, он становится равным 2.
Аналогично предыдущему действию считываем функцию с индек-
сом
t
2
= 2 из табл. 2. Теперь текущая функция (см. табл. 5) имеет сле-
дующий вид:
1
2 3
4
.
F x x x
Далее эта функция раскладывается на подфункции описанным ра-
нее способом.
Чтение из таблицы продолжается, пока значение счетчика
t
2
не пре-
высит значение
t
1
. При этом текущее значение
L
F
является количеством
подфункций в минимизированной формуле. Вид этой формулы легко
восстанавливается из табл. 2.
Заключение.
В работе построен эффективный алгоритм оценки
сложности полинома Жегалкина. Это позволяет в автоматическом ре-
жиме оценивать трудоемкость предполагаемой схемы, что сокращает
общее время разработки схем. Дальнейшие исследования будут на-
правлены на изучение вопросов управления работой алгоритма с уче-
том [8–15], а также применение декомпозиционных преобразований
в соответствующих оптимизационных задачах по методам [16–23],
а также [24–30].
Работа выполнена прифинансовой поддержкеРФФИ№12-01-00710-а.
ЛИТЕРАТУРА
[1] Журавлев Ю.И. Теоретико-множественные методы в алгебре логики.
Про-
блемы кибернетики
, 1962, № 8, с. 5–44.
[2] Кудpявцев В.Б., Гасанов Э.Э., Подколзин А.С.
Введение в теорию интеллек-
туальных систем
. Москва, Изд-во МГУ, 2006, 208 с.


