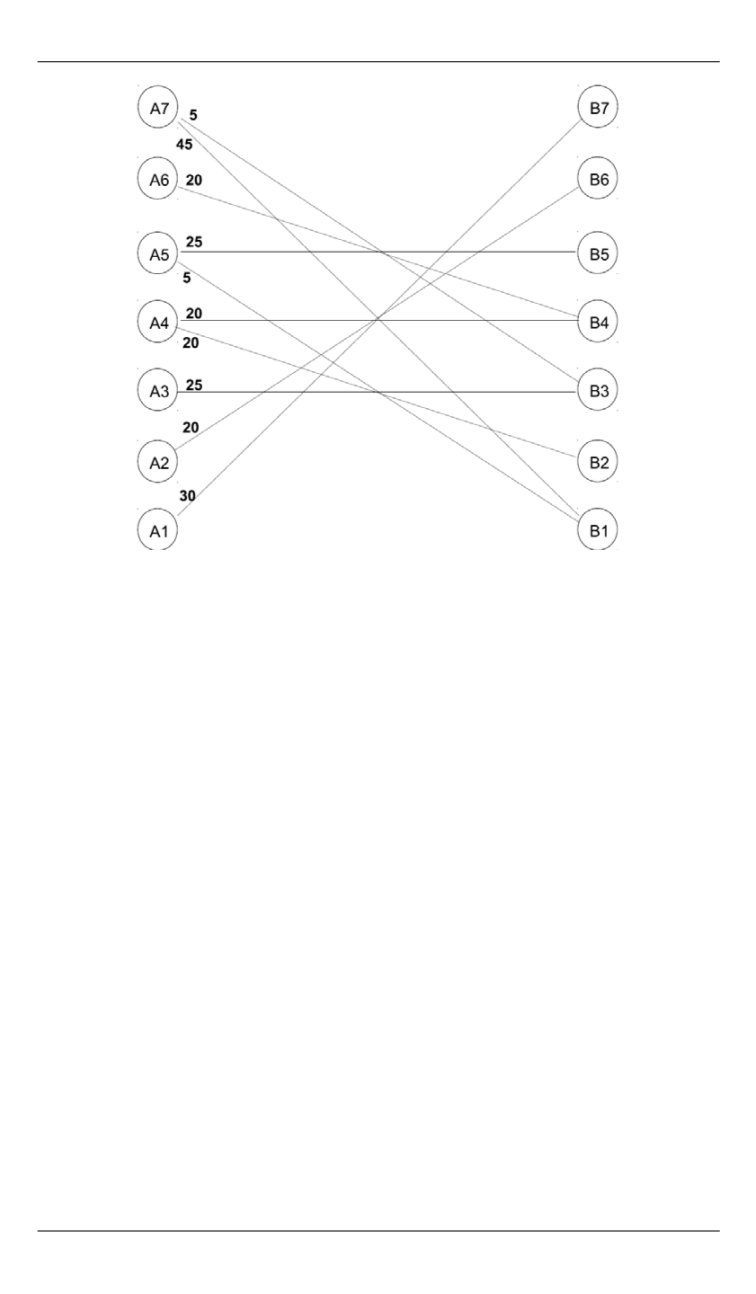
Вычислительные тесты по декомпозиционному алгоритму…
5
Решение транспортной задачи методом потенциалов
Заключение.
Представлены численные расчеты итеративным ме-
тодом для транспортной задачи, когда вычисления осуществляются по
простой схеме без вырождения. Этот случай не является общим. Как
правило, окончательная система линейных алгебраических уравнений
несовместная, алгоритм работает по рассмотренной схеме, но вводятся
обобщенные поставщики и потребители. Дальнейшие численные
расчеты будут относиться к случаю наличия обобщенных поставщиков
и потребителей.
ЛИТЕРАТУРА
[1] Миронов A.A., Цурков В.И. Approximation and Decomposition by Extremal
Graphs.
Журнал вычислительной математики и математической физики
,
1993, т. 33, № 2, с. 34–39.
[2]
Миронов А.А., Цурков В.И. Транспортные и сетевые задачи с
минимаксным критерием.
Журнал вычислительной математики и
математической физики
, 1995, т. 35, № 1, с. 141–147.
[3] Миронов А.А., Цурков В.И. Наследственно минимаксные матрицы в
моделях транспортного типа.
РАН. ТиСУ
, 1998, № 6, с. 67–73.
[4] Миронов А.А., Цурков В.И. Transport-Type Problems with a Criterion.
Автоматика и телемеханика
, 1995, № 12, с. 109–118.
[5]
Миронов А.А., Цурков В.И. Наследственно минимаксные матрицы в
моделях транспортного типа.
РАН. ТиСУ
, 1998, № 6, с. 89–96.
[6] Миронов А.А., Цурков В.И. Транспортные задачи с минимаксным
критерием.
Докл. РАН
, 1996, т. 346, № 2, с. 342–347.
[7] Миронов А.А., Цурков В.И. Network Models with Fixed Parameters in
Coupling Nodes. 2.
Изв. РАН. ТиСУ
, 1993, № 6, с. 3–14.


