В.В. Горский, В.А. Сысенко
4
Здесь
00
h
— энтальпия торможения набегающего воздушного потока;
ekk
h
— определяющая энтальпия Эккерта [9];
r
h
— энтальпия восста-
новления набегающего воздушного потока [2];
w
h
— энтальпия газо-
вой смеси при температуре стенки;
—динамическая вязкость воз-
душной смеси;
Pr
— число Прандтля;
eff
x s
— длина цилиндра,
обтекаемого воздушным потоком с параметрами, соответствующими
точке полусферы с координатой
s
, для которого выполняются следу-
ющие два условия [2]:
удельный тепловой поток в его концевом сечении равен анало-
гичному потоку на полусфере в точке с координатой
s
;
интегральный тепловой поток к поверхности цилиндра равен
аналогичному потоку на поверхности полусферы, ограниченной
сверху сечением с координатой
s
.
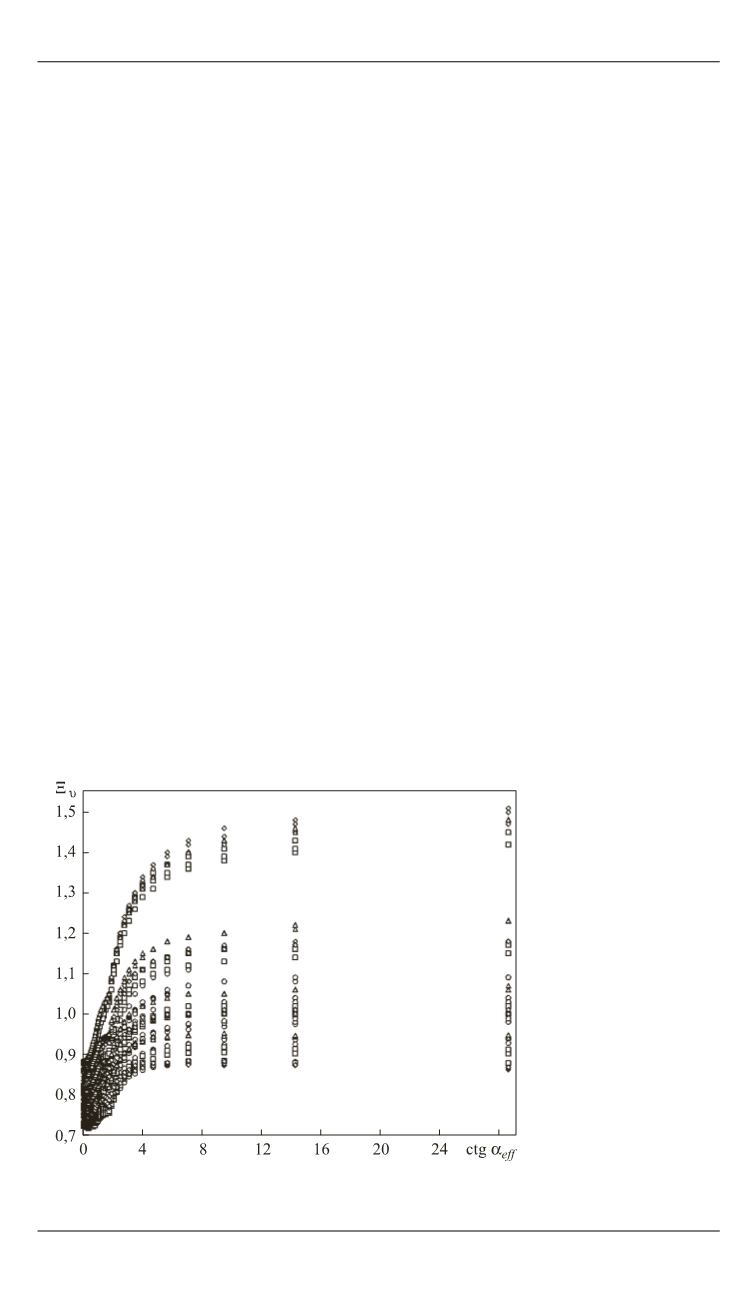
На рис. 1 приведены результаты сопоставления толщины потери
импульса на поверхности полусферы, рассчитанные по формуле (3),
с аналогичными результатами численных решений уравнений погра-
ничного слоя. На рисунке приняты следующие обозначения:
num lit
=
;
2
eff
= s
— эффективный угол атаки, рад;
,
eff lim
max α ; 0, 01
eff
=
— эффективный угол атаки, ограниченный
снизу значением, равным 0,01;
num
— толщина потери импульса,
найденная в результате численного решения уравнений пограничного
слоя.
Рис. 1.
Зависимость
отношения
толщин
потери импульса в ла-
минарном погранич-
ном слое, рассчитан-
ных по формуле (3) и
по результатам чис-
ленного решения урав-
нений пограничного
слоя, от эффективного
угла атаки:
○ —
M
=25, □ — 15,
— 8, ∆ — 4


