Оценка точности инженерных методов расчета…
3
ные по переносным свойствам многокомпонентных воздушных сме-
сей, исследователи были вынуждены использовать для тестирования
инженерных методов расчета теплообмена результаты эксперимен-
тальных исследований, несмотря на их значительный разброс.
В настоящее время ситуация изменилась кардинальным образом. Это
обусловлено тем, что современные численные методы решения урав-
нений пограничного слоя (типа рассмотренных в настоящей работе) и
методы численного решения уравнений Навье — Стокса (см., напри-
мер, работу [5]) позволяют получать достоверную информацию о кон-
вективном теплообмене на поверхностях сложной формы, не говоря
уже о теплообмене в окрестности критической точки сферы.
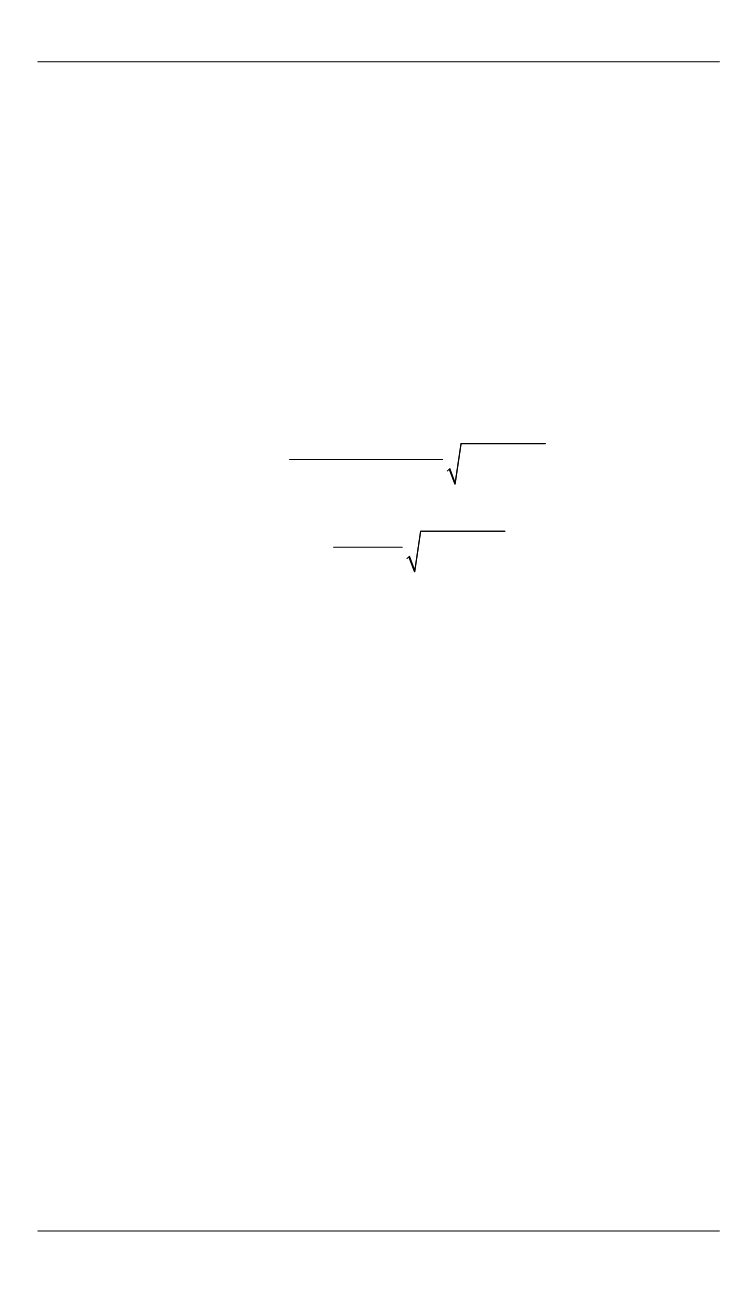
При обработке результатов численных расчетов применяли кри-
терии теплообмена и трения в виде
0
0
00
Cr
Re ,
1
sph
w, n,
R
h, n,
h
q
=
h – R V
;
, ,
, , 0
Cr
Re ,
sph
w n 0
R
f n
e
=
u V
.
Здесь
0
Cr
h, n,
,
, , 0
Cr
f n
— критерии теплообмена и трения на непрони-
цаемой стенке в окрестности критической точки сферы;
0
w, n,
q
,
, , 0
w n
— удельный тепловой поток и напряжение трения на непро-
ницаемой стенке в окрестности критической точки сферы;
00
h
,
e
u
—
энтальпия торможения набегающего воздушного потока и скорость
на внешней границе пограничного слоя;
,V
— плотность и ско-
рость в набегающем воздушном потоке;
Re ,
sph
R
— число Рейноль-
дса, рассчитанное с помощью параметров набегающего воздушного
потока и радиуса сферы
sph
R
.
Построение оптимальных аппроксимационных зависимостей для
расчета критериев теплообмена и трения, базирующееся на результа-
тах систематических численных исследований, проводили в два эта-
па. На первом использовали степенные функции
21,
, , 0 11,
Cr
= M
h
h n
h
; (1)
21,
, , 0 11,
Cr
= M
f
f n
f
. (2)
В табл. 1 приведены оптимальные значения аппроксимационных
коэффициентов
, входящих в эти формулы, которые найдены в со-
ответствии с методом наименьших квадратов одним из вариантов ме-


