А.С. Чуев
8
магнитному потоку
. Линейный характер системных связей подчер-
кивает их аналогию.
На рис. 6 приведена еще одна системная закономерность, обозначен-
ная сплошной красной линией. Она иллюстрирует связь
объемной плот-
ности действия
с
гравитационной постоянной
и полевыми гравитаци-
онными величинами.
Действием
Фейнман назвал ФВ, представляющую
собой произведение
энергии
на
время
и совпадающую по размерности с
моментом импульса.
Поскольку механический
момент импульса
по раз-
мерности равен произведению
импульса
на
длину
, то данная ФВ выража-
ет не только вращательное движение, но и, судя по всему, движение типа
толкательного. А это вполне может служить объяснением свойства инер-
ции, остающееся до сих пор таинственным и непонятным.
По теории С.Г. Тигунцева [7], инерция, именуемая автором
«инерцией-тигунцией», обусловлена силами гравитации, имеющими
всегда центральной характер. По Тигунцеву сила инерции является
непрерывно действующей (интересно, что так же считали и древние
греки). Причем инерционное движение по Тигунцеву происходит не
по прямой, как это обычно представляется, а по поверхности одина-
кового
гравитационного потенциала
.
Согласно приводимой на рис. 6 системной закономерности
(красный параллелограмм) свойство инерции можно объяснить так: в
гравитационном поле с
напряженностью
E
гр
при изменении
скоро-
сти
движения материального тела обязательно возникает и измене-
ние объемной
плотности момента импульса
(
действия
), которое
иначе можно назвать изменением
поверхностной плотности импуль-
са
(
J
гр
на рис. 7). Эта ФВ незримо присутствует всюду, где есть гра-
витационное поле. Причем инерционное действие должна испыты-
вать каждая частичка тела.
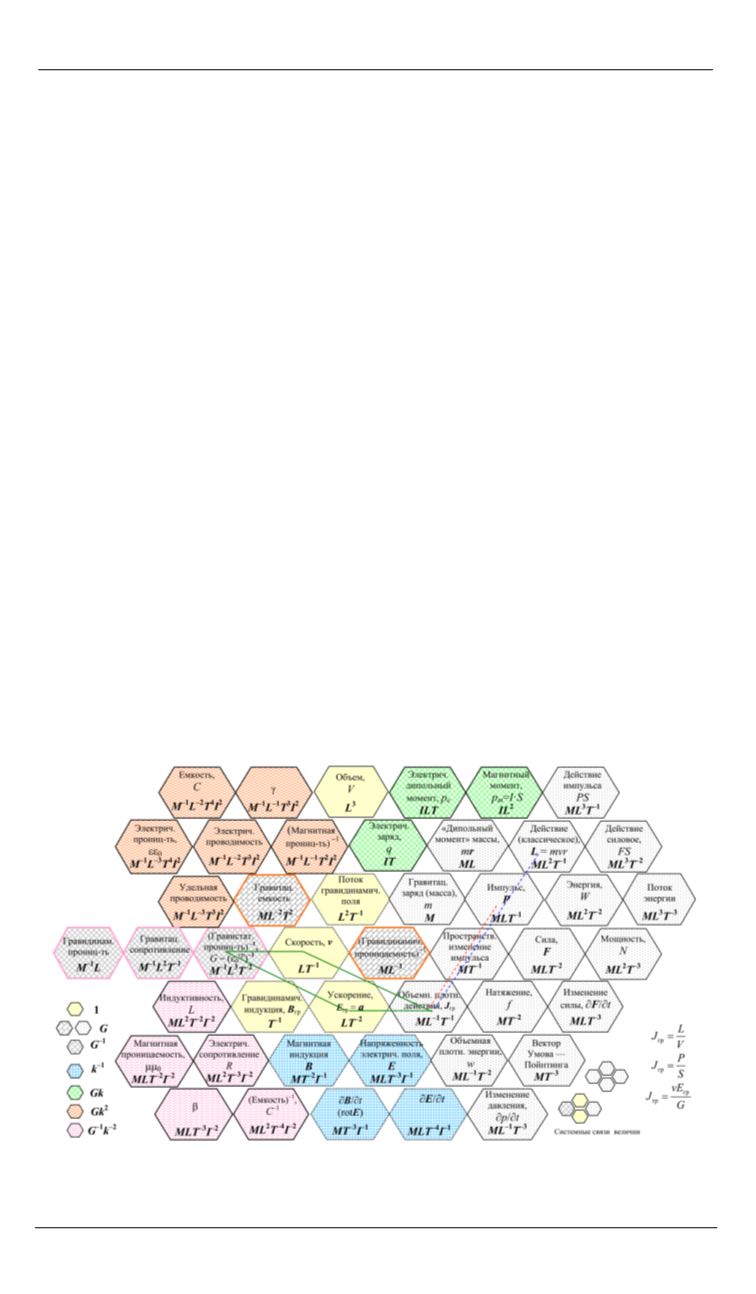
Рис. 7.
Системные связи, поясняющие гравитационное происхождение
инерции и законов сохранения
импульса
и
момента импульса


