А.С. Чуев
6
По рис. 4 численное значение
гравидинамической константы
гр
0
μ
получается путем деления гравистатического
гр 1
0
(ε )
G
(где
G
—
гравитационная постоянная
в системе СИ) на скорость во второй
степени (скорость распространения гравитации, предположительно
равной скорости света). Отметим следующее важное обстоятельство:
если электромагнитные полевые величины не имеют наглядного мо-
дельного представления и они, можно сказать, фантомны (обоснова-
ние приведено в [6]), то в сфере гравитационных величин полевые
ФВ вполне реальны.
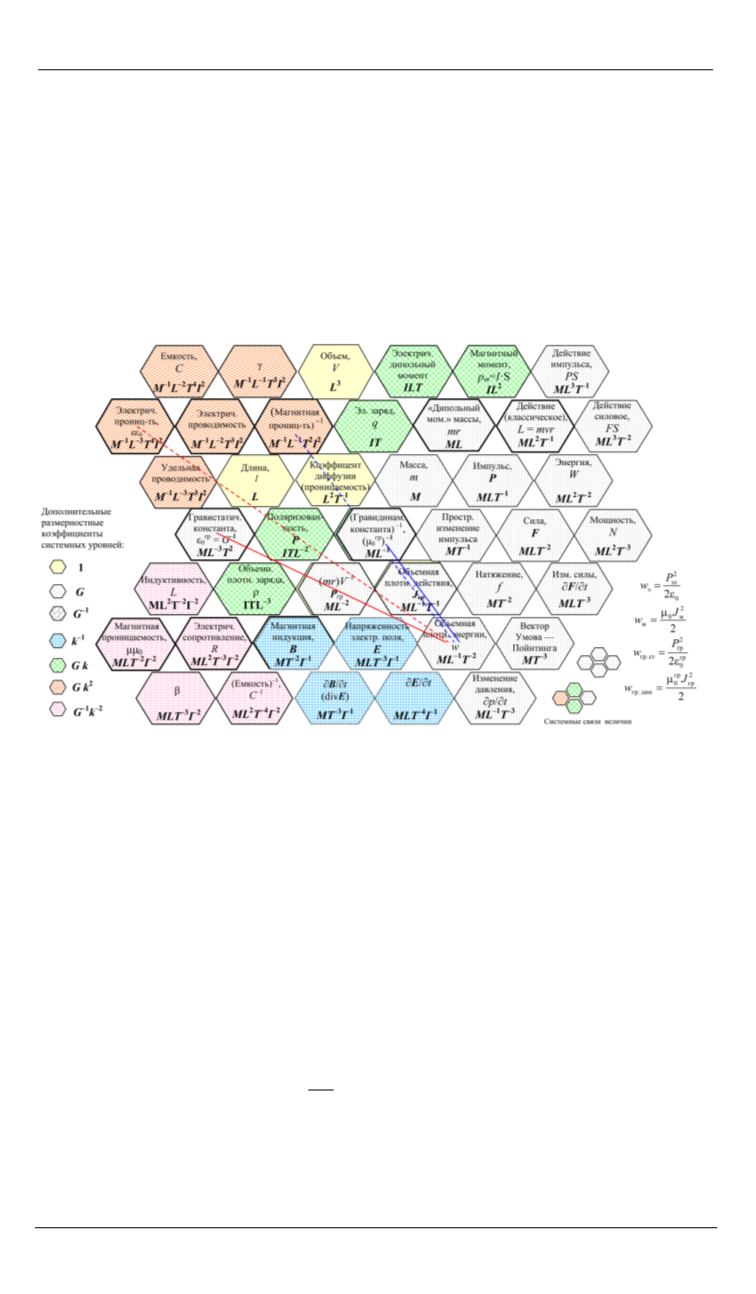
Рис. 5.
Расположение и связи «материальных» полевых величин в сферах
гравитации (сплошные линии) и электромагнетизма (пунктирные линии)
Одно из первых, что бросается в глаза при взгляде на приводи-
мые изображения системы ФВиЗ, — это наличие в системе физиче-
ской величины, представляющей собой произведение
массы
на
длину
(
пространственную протяженность
). На рис. 5 эта ФВ обозначена
как «
Дипольный момент массы
». Данная ФВ непривычна, но дей-
ствительность ее существования подтверждается известным соотно-
шением из микромира [5]. Это соотношение связывает заряд элек-
трона
q
e
, его массу
m
e
, классический радиус электрона
r
e
, скорость
света
с
и электрическую постоянную
0
:
2
2
0
4
.
e
e e
q
r m c
Путем несложных преобразований приводимое соотношение
можно выразить иначе и опять-таки с использованием только фунда-
ментальных физических констант:


