Особый случай малых вынужденных колебаний линейной упругой механической системы
3
Тогда
кр
1
( , )
( ) sin 2 1 cos 2
4
M z t
R z
pt
. (3)
Дифференциальное уравнение малых крутильных колебаний
2
2
2
2
1 ( ) sin 2 (1 cos 2 ),
4
р
J
GJ
R z
pt
p
t
z
(4)
где
GJ
p
— крутильная жесткость стержня.
Из уравнения (4) следует, что вынужденные крутильные колеба-
ния происходят с частотой 2
p
относительно некоторого постоянного
во времени угла
1
( ) 0
z
, за исключением «экзотического» случая,
когда
u
(
z
) подобрана специально.
Обратимся к простейшей постановке задачи, которая, тем не ме-
нее сохраняет суть изучаемого явле-
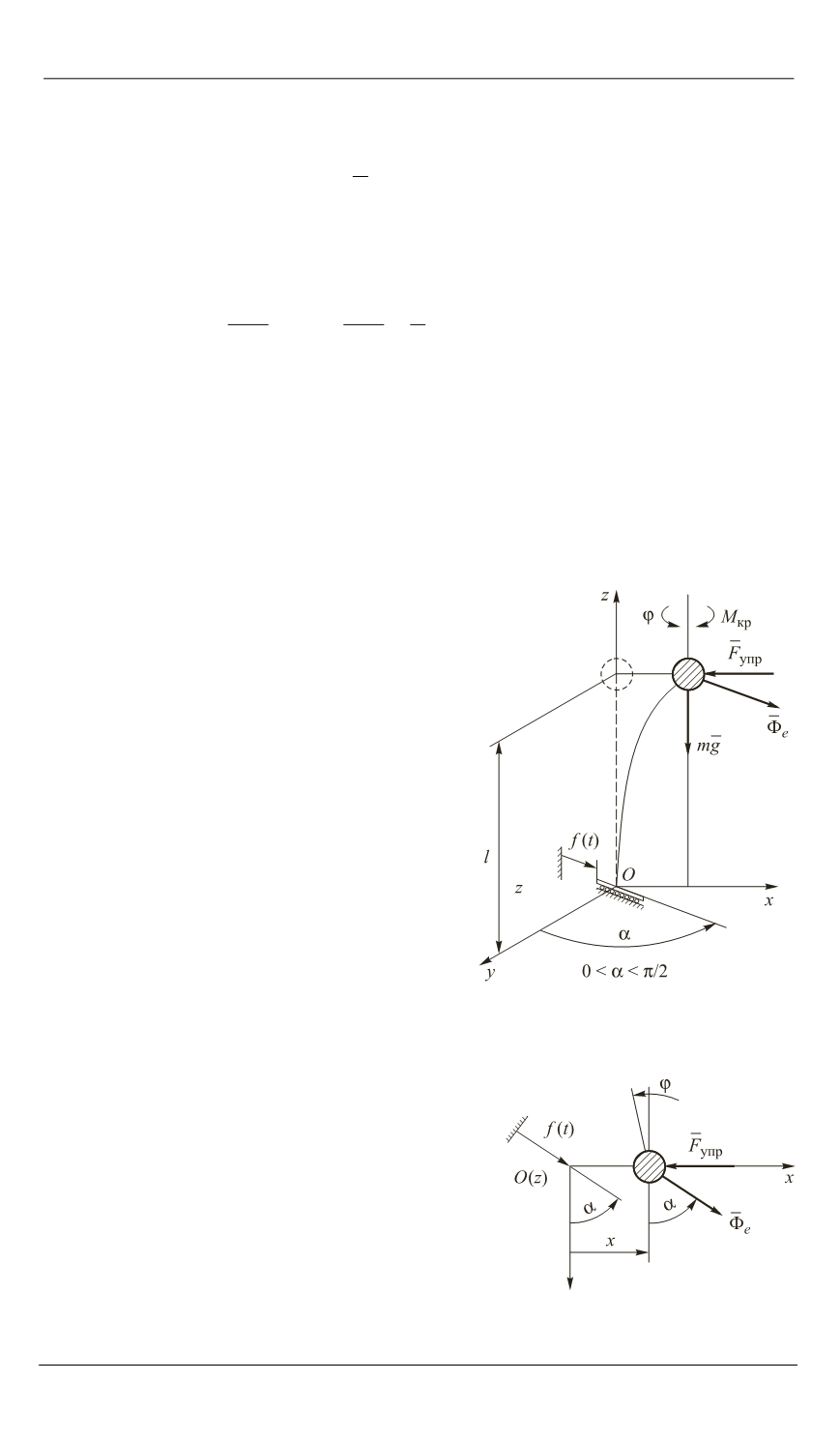
ния. Представим модель консольно
закрепленного стержня (см. рис. 1).
Считаем, что его масса сконцентриро-
вана на верхнем торце. Таким обра-
зом, стержень трансформируется в
невесомую пружину с теми же жест-
костными характеристиками, что и у
стержня. На пружине закреплен объ-
ект, имеющий массу
m
и момент
инерции
J
z
, размерами которого мож-
но пренебречь (рис. 3).
В отличие от силового воздей-
ствия, которое рассматривалось в
предыдущем случае, считаем, что ос-
нование стержня перемещается под
углом
к оси
y
по закону
( ) sin .
f t b pt
Такое возбуждение вы-
нужденных колебаний называют ине-
рционным.
Опишем малые вынужденные ко-
лебания объекта относительно по-
движной системы отсчета
xOyz
, свя-
занной с основанием стержня. Здесь
x
(
t
) и
(
t
) — линейное и угловое пе-
ремещения объекта относительно по-
движной системы отсчета (рис. 3, 4);
Рис. 3.
Рис. 4.


