А.И. Коротаев, В.И. Кузовлев
4
Для определения величин
x
,
y
,
z
предлагается использовать до-
полнительный предмет (например, кубик) с заранее известными па-
раметрами, расположенный рядом с основным объектом (
* *
,
x y
из-
вестны из второй фотографической проекции).
Пусть
z
0
― расстояние до картинной плоскости;
x
,
y
,
z
― коорди-
наты вершин куба в системе координат
X
,
Y
,
Z
; (
x
1
,
y
1
) ―
координаты
вершин куба в исходной фотографической проекции; (
x
*
,
y
*
) ―
коор-
динаты вершин куба в фотографической проекции, полученной в ре-
зультате эволюции аппарата;
x
0
— координата первой вершины куба,
которая должна быть известна.
Координаты точек в фотографической проекции определяются по
формулам:
0
0
1
1
0
0
,
,
1, ..., 6.
i
i
i
i
i
i
z
z
x
x y
y i
z z
z z
Зная
x
0
, определить истинные координаты вершин куба:
1
1
1
1
1
1 01 1
1
0 1 0 1
1
/ ,
(
) / .
y y x x z z y z y y
Остальные пять координат можно определить, решая системы
уравнений:
1
0
0
1
0
0
2
2
2
1
1
1
1,
(
) / ,
(
) / ,
(
) (
) (
)
,
2, ..., 6.
i
i
i
i
i
i
i
i
i
i
i
i
i i
x x z z z
y y z z z
x x
y y
z z
R
i
X
Y
Z
1
2
3
4
5
6
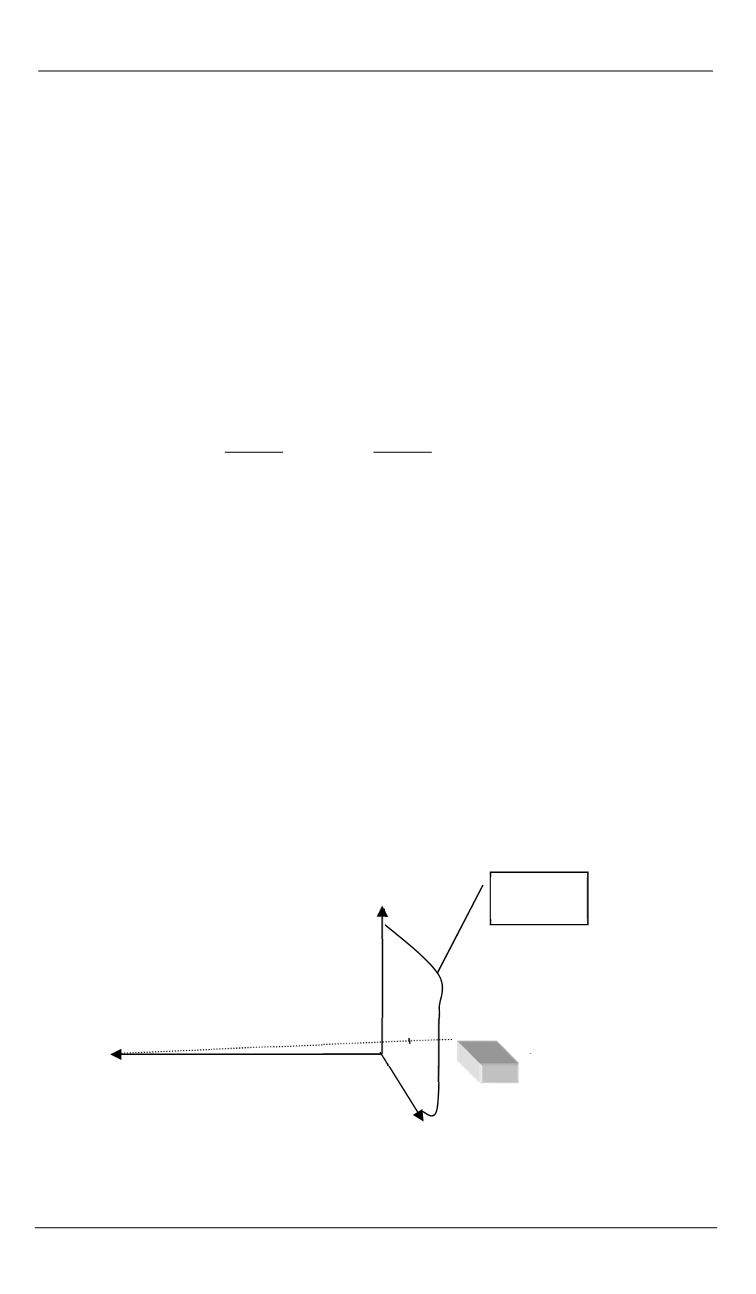
картинная
плоскость
(
x
*
,
y
*
)
(
x
,
y
,
z
)
z
0
Рис.
2.
Использование калибровочного объекта
для определения матрицы преобразования


