В.С. Горелик, В.В. Филатов
6
[30], лагранжиан, описывающий взаимодействие электромагнитного
поля с полем скалярных бозонов, имеет следующий вид:
2 2
1
1
1
(
)
2
4
4
,
m
F F
F F
M
(8)
где
F
μν
− тензор напряжений электромагнитного поля;
F
F
−
дуальный тензор. Первые два слагаемых в соотношении (8) соответ-
ствуют скалярному и электромагнитному полям, третий член задает
взаимодействие между ними, т. е. описывает трехчастичные процес-
сы конверсии двух фотонов вакуума в скалярный бозон (и наоборот).
При этом имеют место законы сохранения энергии и импульса:
;
;
s
u
u
s
u
u
k k k
(9)
;
.
u
u
s
u
u
s
k k k
(10)
Правила отбора разрешают такие процессы для центросиммет-
ричной среды, в том числе и для вакуума. Данный эффект был изучен
с применением лазеров высокой мощности по схеме Light Shining
Through Wall [31] (рис. 4).
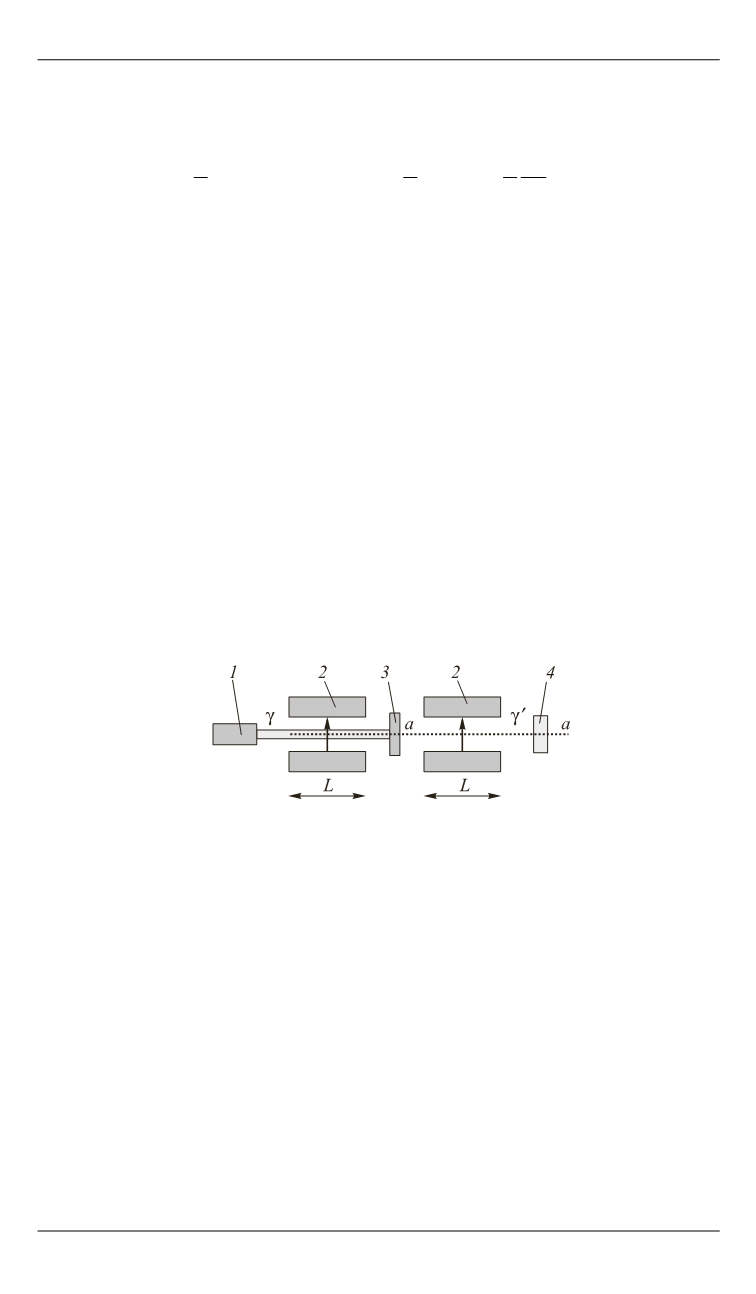
Рис. 4.
Принципиальная схема установки для реализации фотон-аксионной
конверсии:
1
– лазер;
2
– соленоиды;
3
– непрозрачная «стенка»;
4
– приемник излучения;
,
' –
кванты исходного и вторичного излучений;
а
– аксионы (отмечены точками)
Отметим, что для унитарных поляритонов автоматически выпол-
няются условия синхронизма для процесса конверсии двух унитар-
ных поляритонов в скалярный бозон, так как показатели преломле-
ния для обеих частиц равны единице (с точностью до знака). В связи
с этим в данной работе предлагается использовать унитарные поля-
ритоны для реализации процесса конверсии пар поляритонов в ска-
лярный бозон в материальной среде. В этом случае законы сохране-
ния (9) и (10) оказываются выполненными. Кроме того, вероятность
поляритон-бозонной конверсии в материальной среде должна суще-
ственно превышать аналогичную величину в вакууме, так как в мате-
риальной среде возможны процессы типа комбинационного рассея-


