9
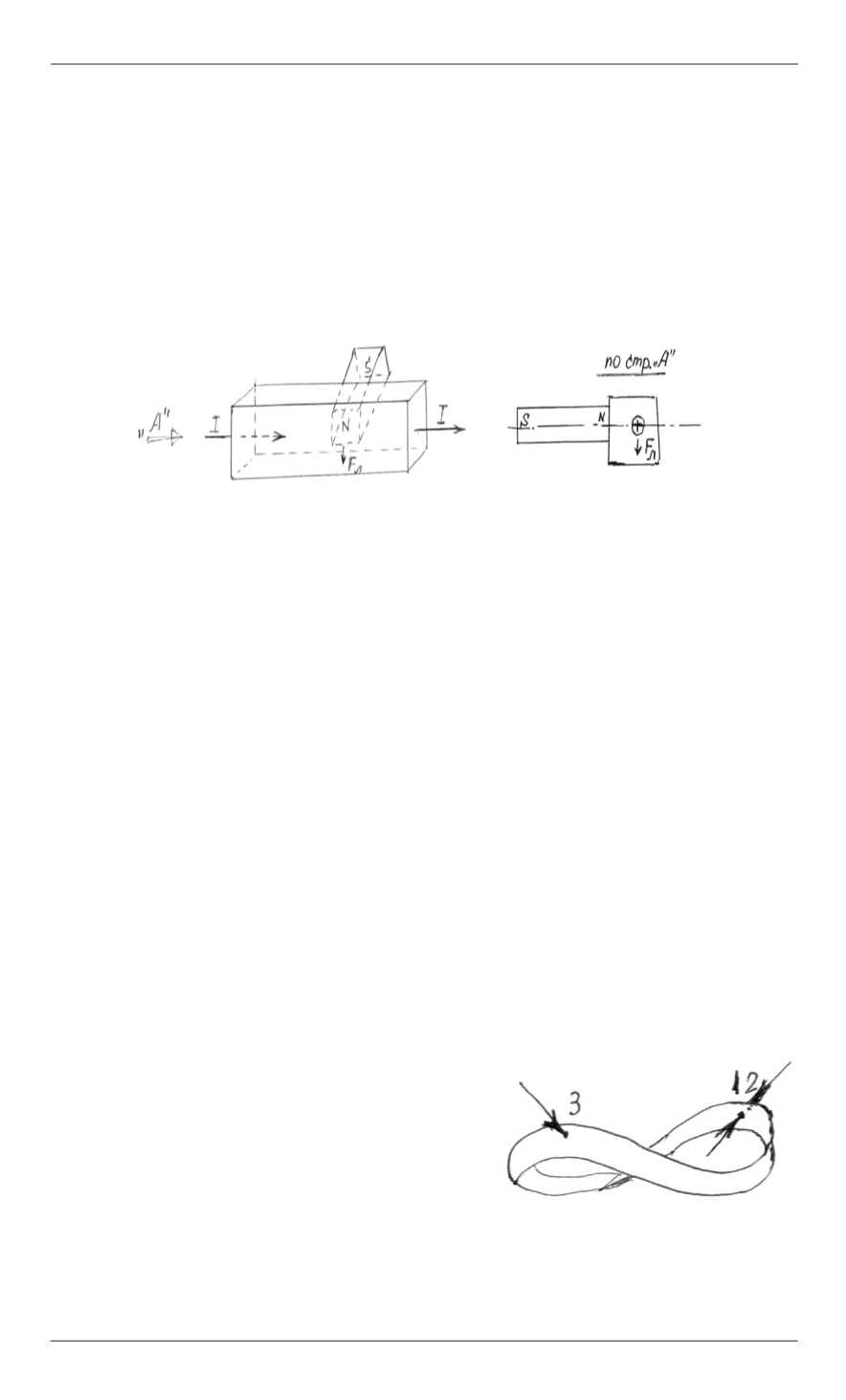
Модель, позволяющая объяснить механизм электромагнитных взаимодействий
заряженных частиц, при движении электронов образуется круговой
поток эфира, который реагирует с потоком эфира, возникающим вокруг
проводника с током (см. рис. 7). В результате образуется пониженное
напряженное состояние в нижней части проводника и повышенное на-
пряженное состояние в его верхней части. Появление поперечной раз-
ности потенциалов под действием магнитного поля было эксперимен-
тально обнаружено Холлом, и в настоящее время этот эффект находит
многочисленные практические применения.
Вращение заряженных частиц.
Лента Мебиуса имеет одну по-
верхность, поэтому при беспорядочных и
редких
ударах различных
частиц электрон приобретает вращательное движение, закручиваясь в
соответствии с правилом правого винта. Однако эта модель предпола-
гает,
что конфигурация заряженных частиц в виде ЛМ при их взаимо-
действии с беспорядочно движущимися эфиронами еще не является
гарантией приобретения заряженными частицами вращательного дви-
жения. Действительно, при оставлении на воздухе демонстрационных
моделей — листов Мебиуса — вращение не происходит, так как при
очень большом числе беспорядочных ударов молекул воздуха каждому
удару в какую-либо точку
1
на ЛМ соответствует одновременный удар
в противоположную точку
2
на ЛМ (рис. 8); в таких условиях эти соуда-
рения взаимно компенсируются. Лишь при сравнительно
редких
соуда-
рениях эфиронов как между собой, так и с электронами, возникают
неодновременные
удары в противополож-
ные точки ЛМ; эти удары, например, в
точку
3
, взаимно не компенсируются и
приводят к возникновению вращательно-
го движения заряженных частиц.
В настоящее время многие разделы
физики оказались неразработанными, и
неясно даже, появятся ли вообще работы,
восполняющие зияющие «бреши». На-
пример, нет вывода закона Кулона, нет
Рис. 8. Возникновение враща-
тельного движения ЛМ под
действием хаотических уда-
ров эфиронов
Рис. 7.
Взаимодействие электрического тока с поперечно рас-
положенным магнитом:
а
— общий вид установки;
б
— вид
по стрелке А


