Тепловая конвекция в замкнутой емкости
5
2
ст
ст
ж
8 ст
9 ст
5 вн ст
2
,
Fo
T
T
T
k
k
k T T
z
r
где
8
ст ст
ж0 ж0
;
k с
c
ст
Т
—
температура стенки;
9
ст ж0
.
k
В начальный момент времени пар и жидкость считаем неподвиж-
ными и имеющими температуру и давление тройной точки. Тепловые
граничные условия известны из постановки задачи. Граничные усло-
вия для функции тока получаем из граничных условий для скоростей:
на твердых поверхностях
—
из условия «прилипания», на границе
пар
—
жидкость — из равенства нормальных и касательных напря-
жений, на оси
—
из условия симметрии. Граничные условия для вих-
ря задаем на вспомогательных поверхностях, отстоящих на один узел
сетки от внешних границ, по методике, предложенной в работе [14].
Задачу решаем численно с применением метода сеток по явной
схеме расчета. В целях улучшения консервативных свойств разност-
ной схемы, а также для выяснения особенностей пограничного тече-
ния жидкой и паровой фаз используем неравномерную сетку с мини-
мальными пространственными шагами вблизи боковой и свободной
поверхностей.
Вопросы устойчивости и консервативности применяемой раз-
ностной схемы рассмотрены в работе [10]. Уравнения Пуассона для
определения вихря решаем итерационным методом переменных
направлений. В области жидкости в вертикальном направлении ис-
пользуем растягивающуюся во времени сетку 32
21 (одинаковую
для областей пара и жидкости).
Расчеты проводим при следующих значениях основных парамет-
ров (для шугообразного азота):
п
h
= 0,3;
ж0
h
= 0,3;
ш0
0, 4
h
;
0
р
= 0,125;
вн
T
= 16,7;
п0
Pr
= 0,89;
ж0
Pr
= 2,28; Ra
п0
= 2,65
10
8
; Ra
ж0
= 10
8
;
1
k
= 16,7;
2
k
= 0,056;
3
k
= 0,04;
4
k
= 0,5;
5
k
= 0,01;
6
k
= 0,194;
7
k
= 4,45;
8
k
= 0,8;
9
k
= 64;
1
А
= –0,36;
2
А
=1,54;
3
А
= –0,187.
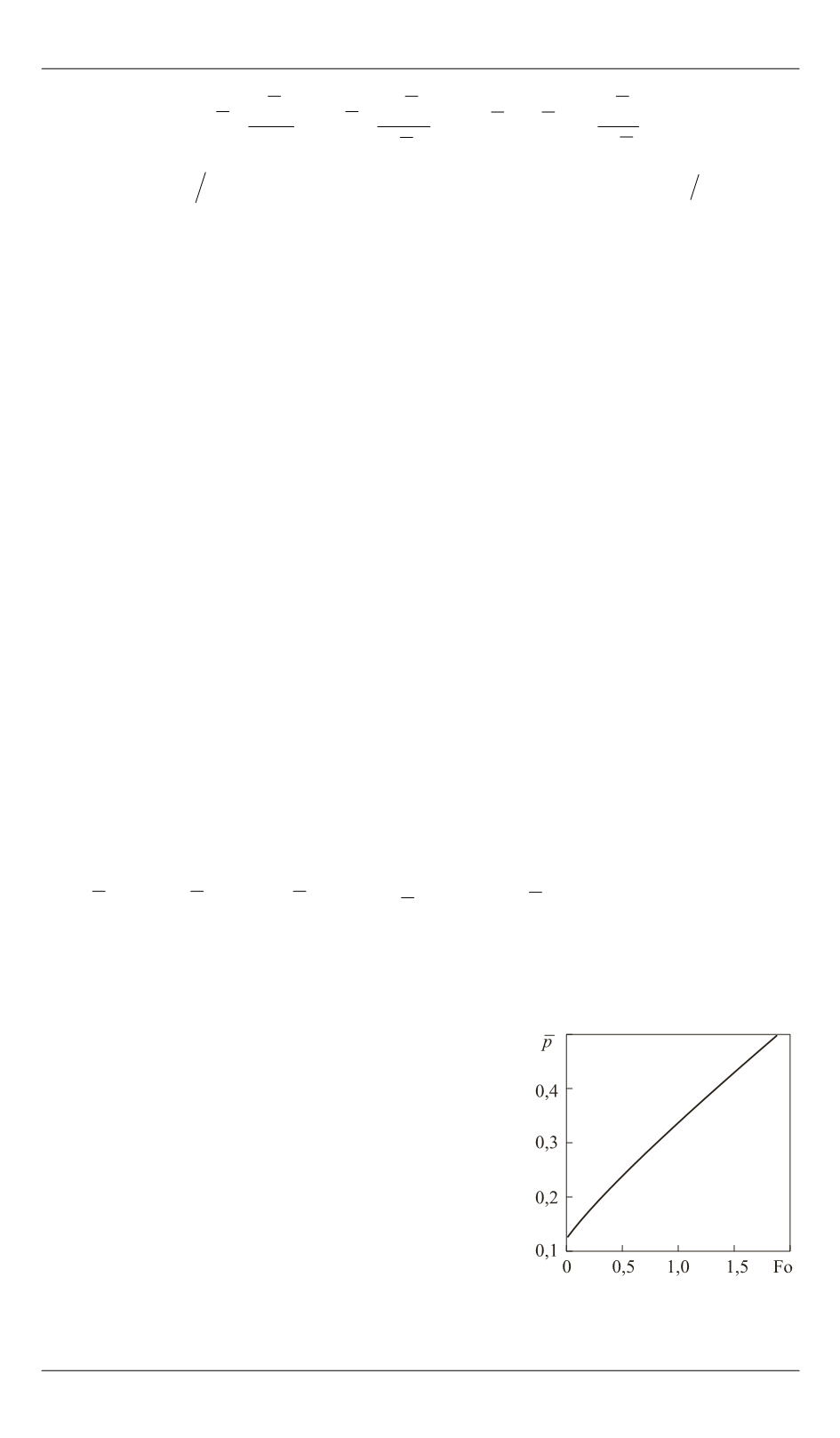
На рис. 2 видно, что зависимость дав-
ления от времени близка к линейной.
Наличие шугообразного продукта и
значительного вертикального градиента
температуры в жидкости и паре приводит к
существенному снижению интенсивности
конвективного движения (рис. 3 и 4). Вли-
яние конвекции на температурное поле
проявляется в узкой зоне, прилегающей к
Рис. 2.
Изменение давле-
ния в емкости во времени


