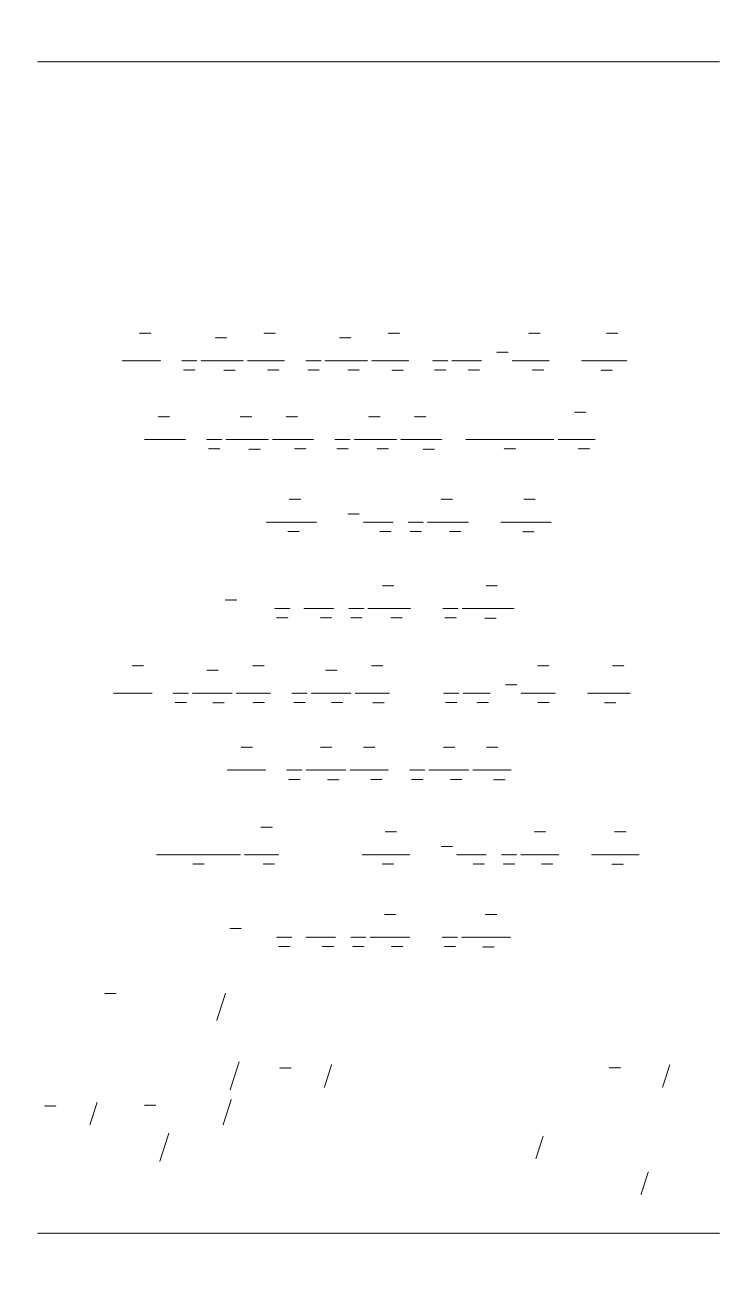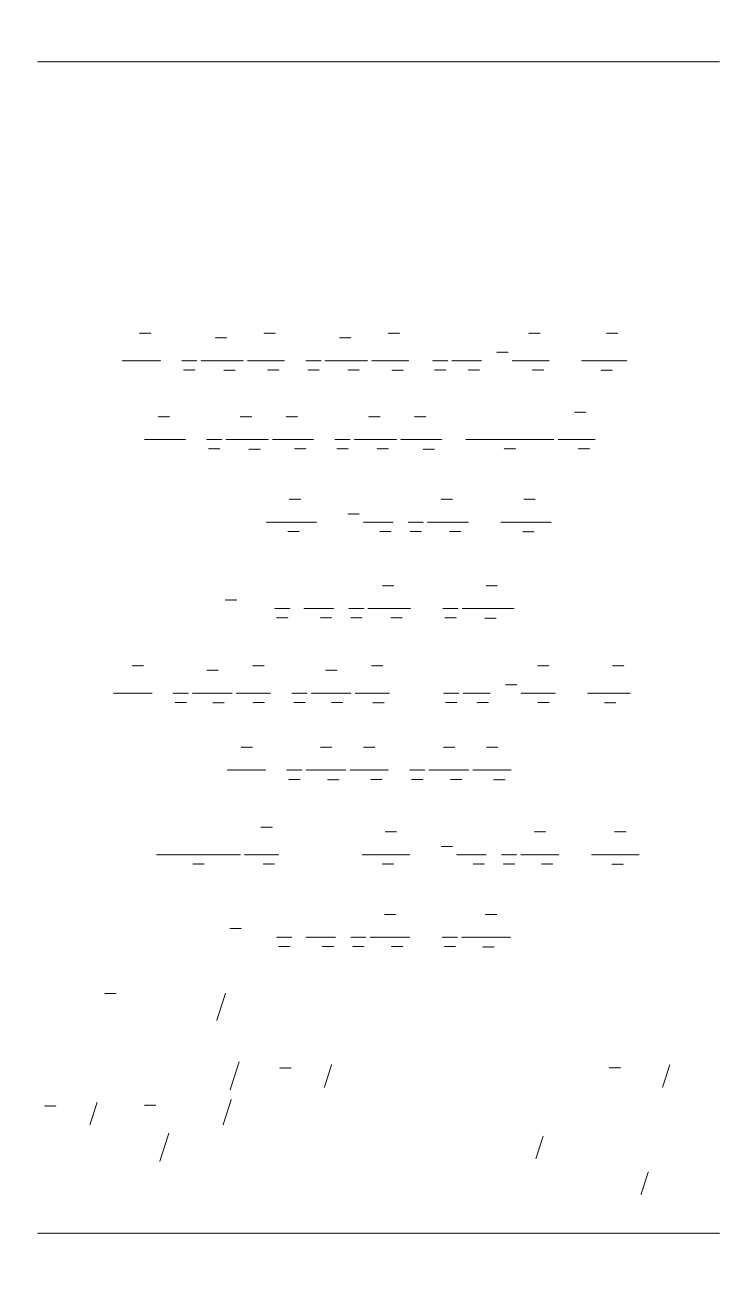
Тепловая конвекция в замкнутой емкости
3
Численные методы решения задач тепловой конвекции рассмот-
рены в работах [5
–
10], а методика расчета положения подвижной
границы с учетом плавления твердой фазы
—
в работах [11, 12]. В
работе [13] приведены результаты численного решения задачи о ро-
сте давления в одномерной замкнутой области, частично заполнен-
ной шугообразным продуктом.
Используя приближение Буссинеска и переменные вихрь
—
функция тока, запишем систему дифференциальных уравнений энер-
гии и движения в области жидкости и пара в безразмерном виде:
2
ж
ж ж
ж ж
ж
ж
2
1
1
1
;
Fo
T
T
T
T
T
r
r z r r r z r r
r
z
ж
ж ж
ж ж
ж0 ж0 ж
1
1
Ra Pr
Fo
T
r z r r r z
r
r
2
2
ж
ж
ж
ж0
2
2
1
Pr 4
3
;
r
r
r r r
z
2
ж
ж
ж
2
1
1
1
;
r r r r
r z
2
п
п п
п п
п
п
1
2
1
1
1
;
Fo
T
T
T
T T
k
r
r z r r r z
r r
r
z
п
п
п
п
п
1
1
Fo
r z r r r z
2
2
п0 п0 п
п
п
п
1 1
п0
2
2
Ra Pr
1
Pr 4
3
;
T
k k
r
r
r
r
r r r
z
2
п
п
п
2
1
1
1
.
r r r r r z
Здесь
тт
0
;
T T T
тт
T
—
температура тройной точки;
0
0 ж
;
T T
0
T
—
начальная температура;
ж
T
—
температура жидкости; Fo
—
число
Фурье,
2
ж0
Fo
;
a t R
;
r r R
—
функция тока;
0
Ra ;
;
z z R
3
0
;
R a
—
вихрь; Ra
0
—
число Рэлея,
0
Ra
3
0 0 0
0 0
;
g
R a
Pr
—
число Прандтля,
0 0
Pr
;
a
—
вязкость;
а
—
температуропроводность;
п
T
—
температура пара;
1
п0 ж0
.
k a a