С.А. Ивлиев
,
А.А. Павельев
,
Н.Ю. Рязанова
6
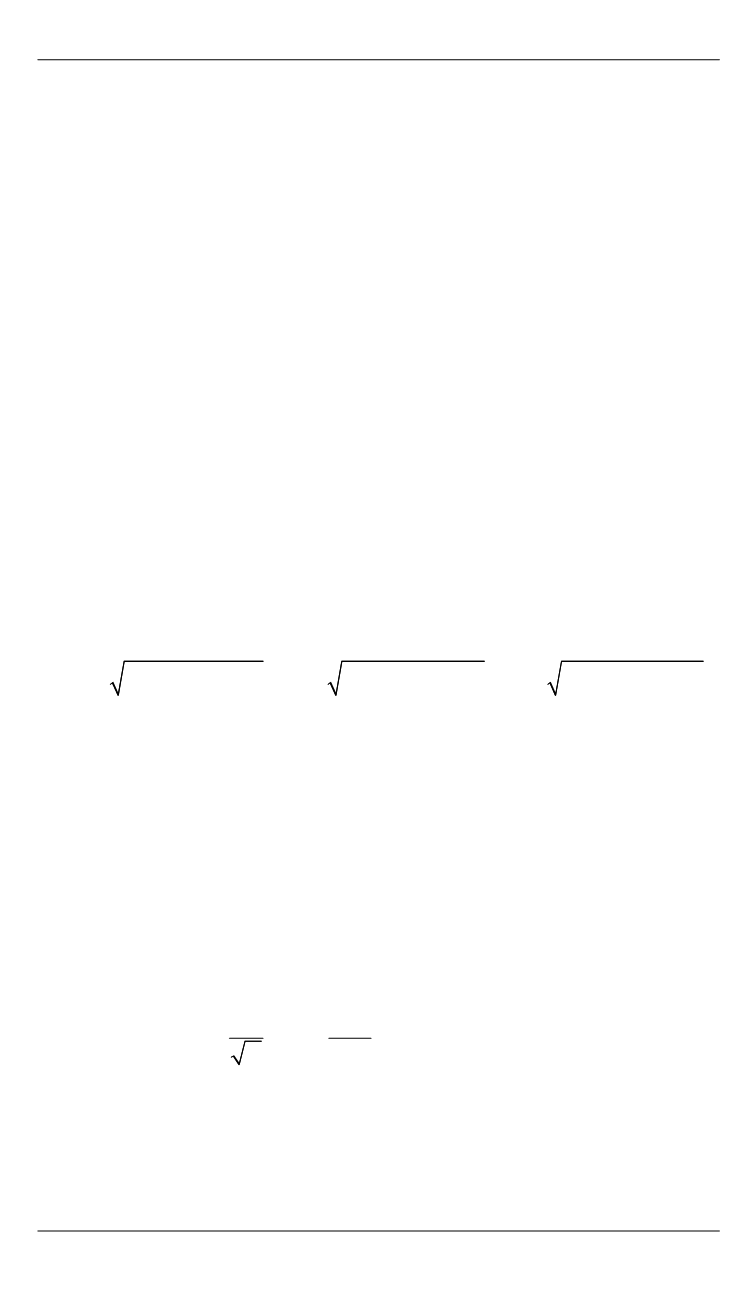
Если поворот задан кватернионом
q
= (
w
,
x
,
y
,
z
), то матрица по-
ворота будет иметь следующий вид:
2
2
2
2
2
2
1 2 2 2 2
2 2
0
2 2
1 2 2 2 2
0
(α)
2 2
2 2 1 2 2 0
0
0
0
1
y z
xy zw xz yw
xy zw x z
yz xw
М
xz yw yz xw x y
⎛
⎞
− −
−
+
⎜
⎟
+
− −
−
⎜
⎟
= ⎜
⎟
−
+
− −
⎜
⎟
⎜
⎟
⎝
⎠
.
В результате умножения матриц получим матрицу совмещенного
преобразования, которую обозначим как
11 12 13
21 22 23
31 32 33
41 42 43
0
0
0
1
m m m
m m m
M
m m m
m m m
⎛
⎞
⎜
⎟
⎜
⎟
=
⎜
⎟
⎜
⎟
⎝
⎠
.
Получив результирующую матрицу, выполним ее декомпозицию
для получения кватерниона. Для этого сначала найдем модуль строк
матрицы [3] и тем самым определим масштабные коэффициенты:
2
2
2
11 12 13
x
k m m m
= + +
,
2
2
2
21 22 23
y
k
m m m
= + +
,
2
2
3
31 32 33
z
k m m m
= + +
.
Затем для получения кватерниона
q
= (
W
,
X
,
Y
,
Z
) выполним сле-
дующие действия:
– разделим каждую строку матрицы на соответствующий мас-
штабный коэффициент и получим матрицу
M
' = {
a
ij
};
– в преобразованной матрице вычисляется сумма элементов
главной диагонали:
'
'
'
11 22
33
1;
T m m m
= + + +
если
T
> 0, тогда
'
'
32 23
'
'
'
'
13 31
21 12
0,5
0, 25
,
,
(
) ,
(
) ,
(
) ;
S
W X m m S
S
T
Y m m S Z m m S
=
=
= −
= +
= +
если T ≤ 0, тогда в главной диагонали необходимо найти максималь-
ный элемент. В зависимости от того, в каком столбце матрицы он
находится, выполняются следующие действия:


