Т.Н. Романова
,
Б.Е. Винтайкин
,
А.М. Зинченко
10
давления шумов применима интерполяция сплайнами или многочле-
ном Лагранжа.
2. Необходимо разбить весь отрезок рентгенограммы на такие от-
резки, на каждом из которых исследуемая функция была бы унимо-
дальной. Иными словами, необходимо выделить на рентгенограмме
области, содержащие по одному максимуму интенсивности каждая.
Эта задача не требует специального алгоритма. К каждой такой обла-
сти применяют один из методов поиска точки экстремума унимо-
дальной функции. Это может быть метод деления отрезка пополам,
золотого сечения или поразрядного поиска.
3. Когда точка максимума известна, необходимо найти дифрак-
ционную линию, т. е. абсциссу 2
θ
, соответствующую максимуму
дифракции. Из-за разного рода погрешностей при проведении экс-
перимента эта линия может не совпадать с максимумом интенсив-
ности, поэтому для более точного ее нахождения используется
один из следующих методов. Первый метод состоит в том, что че-
рез точки, лежащие по разные стороны от пика интенсивности, но
на одной ординате, проводят горизонтальные линии. Далее поло-
жения по оси
x
этих линий усредняют, что и даст положение ди-
фракционной линии [2].
Второй, более распространенный, способ
состоит в определении центра тяжести полу-
ченной спектральной линии, положение ко-
торого по оси
x
выбирается за положение
дифракционной линии. Для этого необходи-
мо определить две крайние точки по обе сто-
роны от пика, составляющие «подножие»
линии. Они будут определять высоту фона
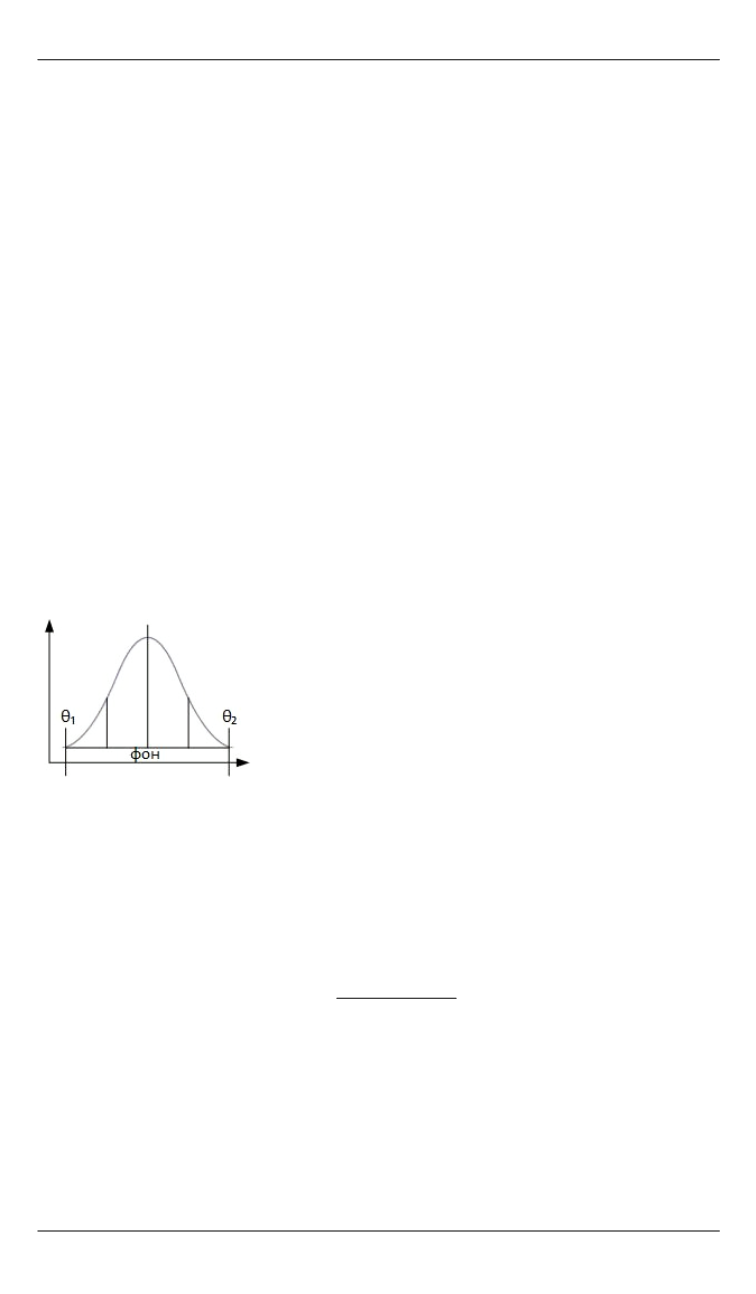
рентгенограммы и ширину линии. Спек-
тральная линия изображена на рис. 6.
Зная ширину, можно найти центр тяжести, используя следующую
формулу [3]:
2
1
2
1
θ
(θ) θ θ
θ θ
,
θ
(θ) θ
θ
с
I
d
I d
⋅ ⋅
∫
=
∫
где
θ
— угол поворота детектора;
I
— зарегистрированная в этом по-
ложении детектора интенсивность рентгеновского излучения за вы-
четом фона;
θ
c
— положение центра тяжести по оси
х
;
θ
1
,
θ
2
— край-
ние точки, определяющие пределы спектральной линии.
Рис. 6.
Спектральная
линия и ее границы


