О проблеме потери геометрической точности…
3
Для построения изогипс существует несколько алгоритмов, реали-
зованных в автоматических программных средствах формирования
рельефа. В частности, популярная программа Surfer
®
12 компании
Golden Software Inc [4] предлагает применять методы Inverse Distance
to a Power, Kriging, Minimum Curvature, Nearest Neighbor, Radial Basic
Functions, Shepard’s Method, Triangulation Linear Interpolation (названия
приведены в соответствии с наименованиями методов Surfer
®
12) [4].
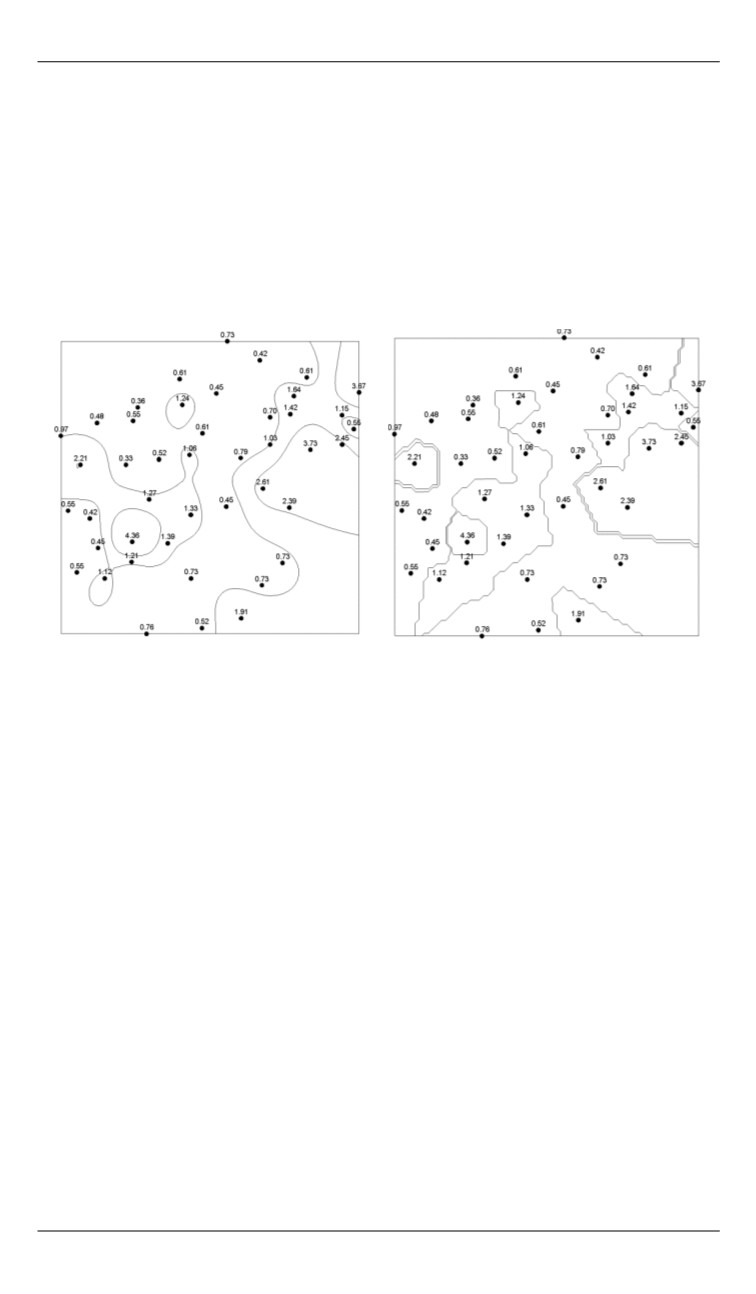
На рис. 3 приведены результаты построения изогипс двумя произволь-
но выбранными методами: Kriging и Nearest Neighbor.
а
б
Рис. 3.
Построение изогипс по методам кригинга (Kriging) (
а
)
и ближайшего соседа (Nearest Neighbor) (
б
)
Анализ рис. 2 и 3 показывает существенную зависимость геомет-
рической точности слоя рельеф от выбора автоматизированного ме-
тода построения изолиний.
Кроме того, при генерализации рельефа изменяется шаг одинако-
вых уровней. При переходе, например, к карте более крупного мас-
штаба, шаг уменьшается, линий одного уровня становится больше, и
вдоль тальвега (пониженное место рельефа местности) они приобре-
тают характер сильно вытянутых замкнутых полилиний. Такой тех-
нический прием правдоподобно передает особенности рельефа, но
для определения морфометрических характеристик горизонтали не-
пригоден. В этом случае карты крупного масштаба, полученные по-
средством картографической генерализации, оказываются неинфор-
мативными.
Выбор метода описания рельефа.
Сравнительный анализ методов
построения линий одинакового уровня по набору точек показывает, что
предпочтение следует отдать параметрическим методам, в частности,
методу обратных расстояний (Inverse Distance to a Power) (рис. 4).


