В.А. Брусов, В.Н. Наумов, Д.А. Чижов, А.А. Долгополов, Ю.Ю. Мерзликин и др.
4
В эту систему уравнений входят величины:
sin
x
G mg
— сила
тяжести, спроецированная на ось
O ;
g
x
cos
y
G mg
— сила тяже-
сти, спроецированная на ось
O ;
g
y
Т
— суммарная тяга маршевых дви-
гателей ЛА;
h
— плечо действия силы тяги
T
относительно центра
масс
ЛА;
j
f
— коэффициент сопротивления
j
-го колеса при касании
опорной поверхности;
ст
,
j
yj
x L
— координаты колесного шасси отно-
сительно центра масс самолета в связанной системе координат
(см. рис. 1);
1, 2, 3
j
— номера амортизационных стоек.
Перемещение штока гидроцилиндра
j
-й стойки
ст
j
y
можно за-
дать через перемещение центра масс ЛА, профиль неровности, а так-
же обжатие грунта и пневматика колеса шасси (см. рис. 1):
к
ст
ст 0
ст
гр
ш пр
sin
ε ε
.
2
j
j
j
j
j
j
j
D
y a L y x
y
Неровность опорной поверхности полосы ВПП задается гармо-
нической функцией [2]:
max
пр
2
1 cos
,
2
x
j
j
H
v
y
t
L
где
max
H
— максимальная
высота неровности;
j
ст
2
j
x L
— отставание
по фазе для
j
-й стойки от-
носительно центра тяжести
самолета.
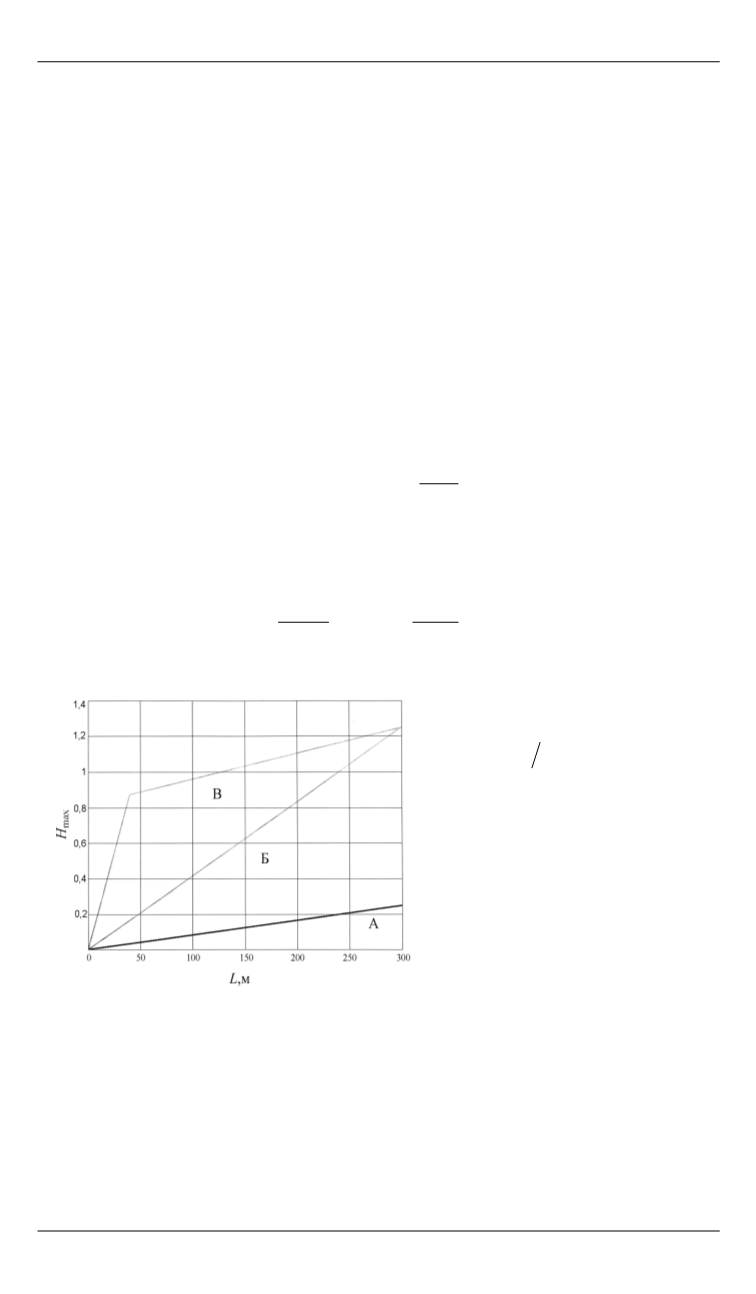
Соотношение
высоты неровности
max
H
и
длины
H
ее профиля опре-
деляют по графику (рис. 2).
При этом выделяют три ти-
па ВПП: зона А — хорошо
подготовленные
полосы
(бетонные), зона Б —
слабо подготовленные по-
лосы, зона В — неподго-
товленные полосы.
Исследования по раз-
работке методики и алгоритмов управления характеристиками амор-
тизационных стоек шасси при разбеге и пробеге по неровной ВПП
Рис. 2.
Классификация ВПП по длине
и ширине неровности:
А— ВПП с твердым покрытием; Б — слабо
подготовленные ВПП; В— неподготовленные
ВПП


