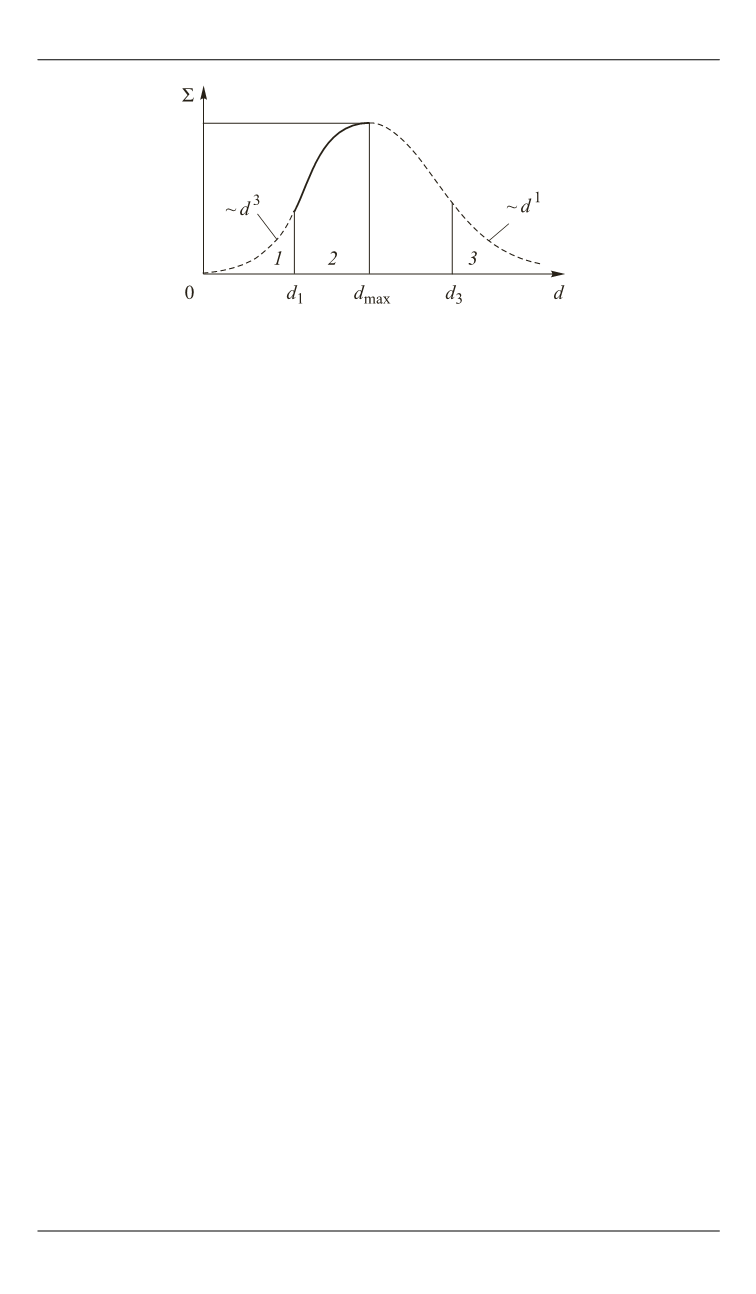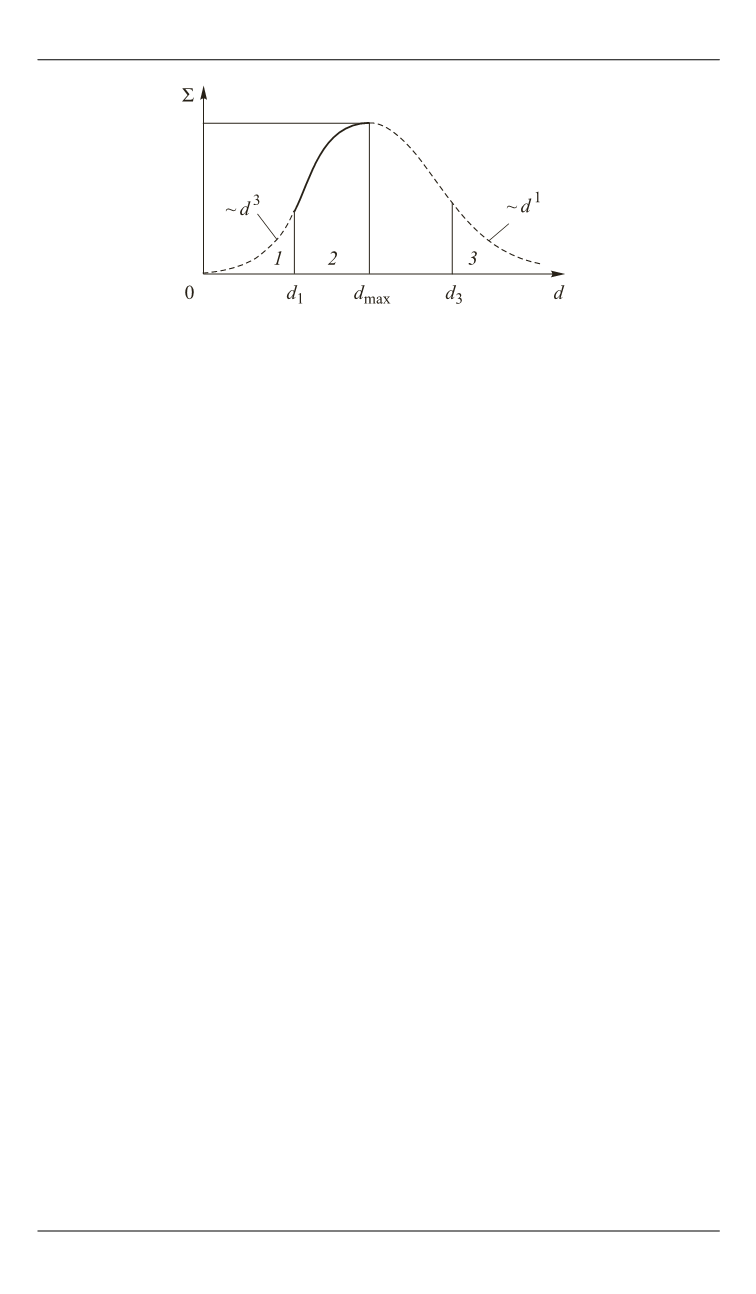
Р.Ю. Герасимов, В.Н. Бовенко, М.Ю. Герасимов
8
Рис. 5.
Схематическая иллюстрация зависимости суммарного значения
«эффективного сечения» рассеяния (и поглощения) единицей объема от
размера частиц порошка (штриховая кривая соответствует теоретическим
оценкам, сплошная – экспериментальным данным)
атомы частиц излучают электромагнитные волны с близкими фазами.
В этом случае интенсивность рассеянного излучения
I
и «эффектив-
ное сечение» рассеяния (и поглощения) σ, как известно, пропорцио-
нальны
N
2
(
N
– число атомов в частице), а
N
, в свою очередь, пропор-
ционально
d
3
. Тогда суммарное сечение рассеяния (и поглощения)
единицей объема Σ = σ
n
(
n
– число частиц в единице объема). По-
скольку
n
~ 1/
d
3
, получаем
I
~ σ ~
N
2
~
d
6
,
I
S
~ Σ = σ
n
~
d
3
.
(6)
Отсюда следует, что в области
1
удельная интенсивность излуче-
ния
I
S
~
d
3
, а амплитуда сигналов
А ~ d
3/2
. С учетом фрактальной раз-
мерности частиц порошка эта зависимость может быть еще более
слабой (
А << d
3
/
2
). При
d >
λ ситуация изменяется: в процессах по-
глощения и рассеяния принимают участие только атомы, располо-
женные на поверхности частиц. В этом случае суммарное «эффек-
тивное сечение» поглощения и рассеяния примерно равно попереч-
ному сечению частицы, т. е.
σ
~ d
2
, а σ
n ~
1/
d
. Поэтому эффектив-
ность рассеяния единицей объема достигает максимума при
d
max
.
Таким образом, при размерах частиц, меньших λ, формирование
спектра сигналов в СВЧ-диапазоне обусловлено эффектами усили-
вающейся интерференции при увеличении размеров частиц. Отме-
тим, что термин «усиливающаяся интерференция» был введен Р.
Фейманом при рассмотрении рассеяния света на микрочастицах кон-
денсированного вещества, представляющих собой большое скопле-
ние атомов, например в виде капелек жидкости, которые возникают в
атмосфере за счет конденсации [15].
На рис. 6 представлена линейная зависимость средних частот
спектра сигналов, полученных в результате расчетов по формуле (5),
от преимущественных размеров частиц. Это позволяет найти среднее