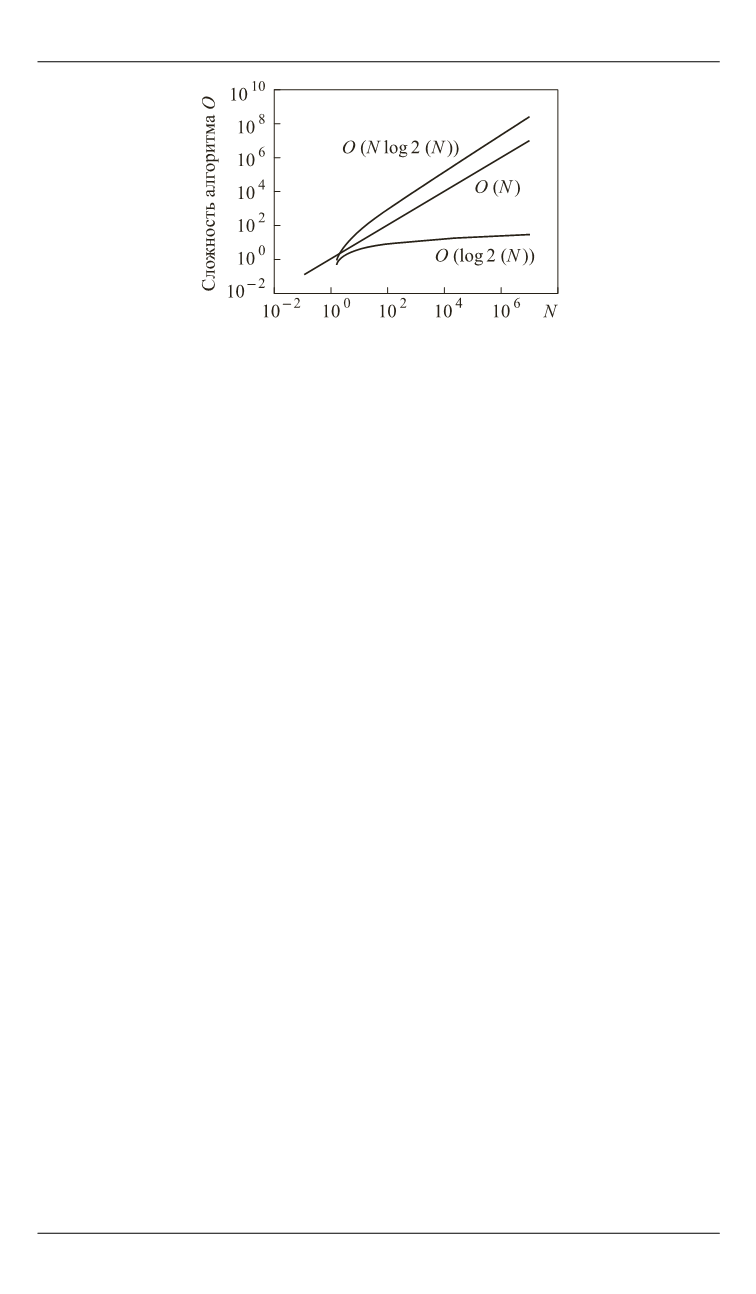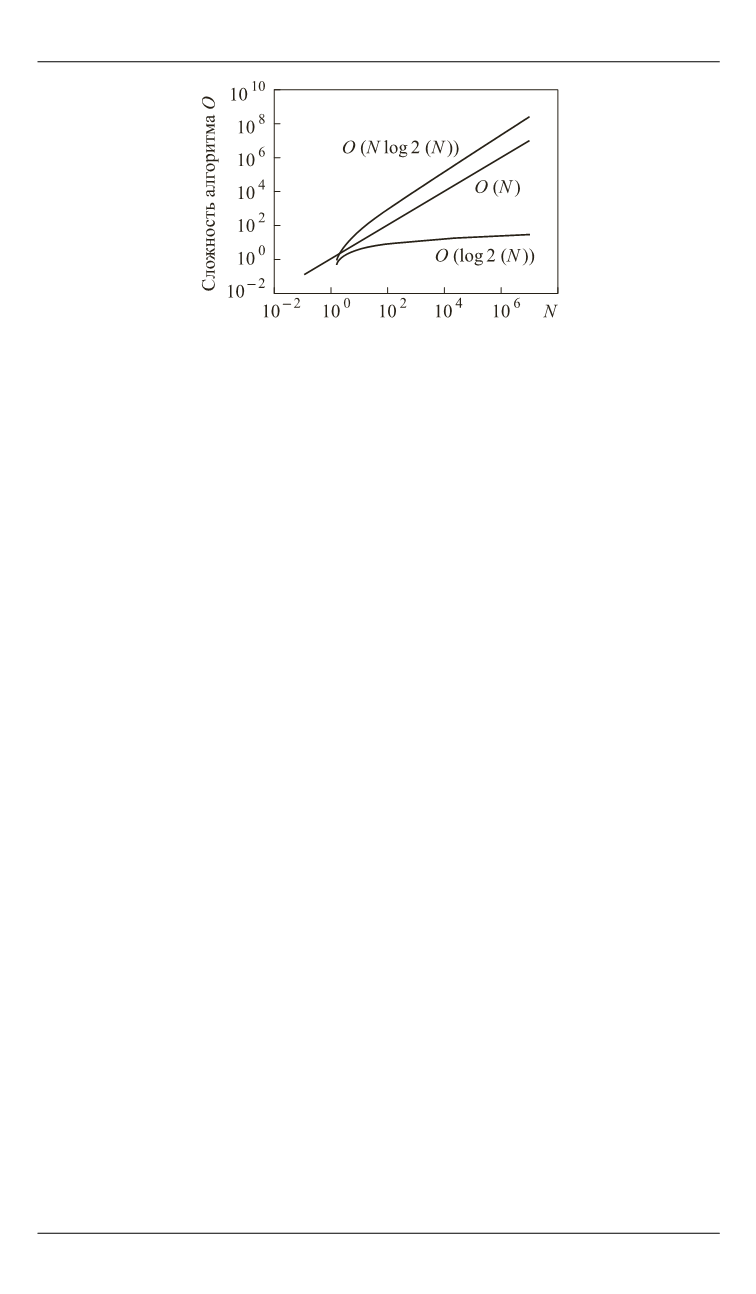
Алгоритм параллельной агрегации данных для визуализации данных о вербальном…
7
Рис. 4.
Сложность алгоритмов при последовательной и параллельной
реализации (красным и синим показаны соответственно наихудший и
наилучший случаи параллельной реализации; зеленым —
случай последовательной реализации)
Оценить сложность алгоритма дерева редукций при параллель-
ной реализации несколько сложнее, чем при последовательной, так
как заранее неизвестно, сколько потоков будет выполняться парал-
лельно. Этот факт зависит от таких параметров и архитектуры кон-
кретного графического процессора (GPU) [9] (в скобках указаны до-
ступные на сегодняшний день значения), как:
•
количество потоков на один мультипроцессор (768, 1024, 1536);
•
количество блоков потоков (
thead block
) на один мультипроцес-
сор (8,16);
•
число мультипроцессоров (16, 30);
•
объем разделяемой памяти (
shared memory
) (16, 32 Кб);
•
количество регистров на один мультипроцессор (8192, 16384,
32768),
а также от других параметров.
В худшем случае, т. е. при последовательном выполнении ин-
струкций каждого блока, сложность алгоритма
log
O N N
. В луч-
шем случае, т. е. при параллельном выполнении инструкции всех
блоков, сложность алгоритма
log
O N
(см. рис. 4).
Одной из задач данной работы является стремление сложности к
log
O N
. Для поиска минимума и максимума по алгоритму дерева
редукций необходимо:
•
инициализировать адресное пространство в глобальной памяти
GPU
;
•
разделить входной массив на блоки данных в соответствии с
моделью M
S
так, чтобы количество блоков данных было равно
ширине окна в пикселах
W
;
•
вычислить локальный минимум на каждом блоке.