В.А. Овчинников, Г.С. Иванова
2
Оптимизирующие преобразования уровня универсального языка
хорошо исследованы [1–3] и реализованы в компиляторах современ-
ных языков, таких как
Delphi Pascal
,
Visual C
++ и т. п. В настоящей
статье рассматривается класс специализированных оптимизирующих
преобразований алгоритмов на графах и множествах. Формализация
таких преобразований авторам не известна. Поскольку эти преобра-
зования основаны на исследовании процесса трансформации модели
исходного описания объекта в модель результата, их целесообразно
выполнять при описании алгоритмов на уровне множеств и/или гра-
фов [4, 5].
Цель работы — показать возможность формализации оптимизи-
рующих преобразований, связанных со свойствами операций над
предикатами и множествами, и синтезировать соответствующие пра-
вила.
Ниже представлены некоторые результаты выполненного авто-
рами анализа способов снижения вычислительной сложности, харак-
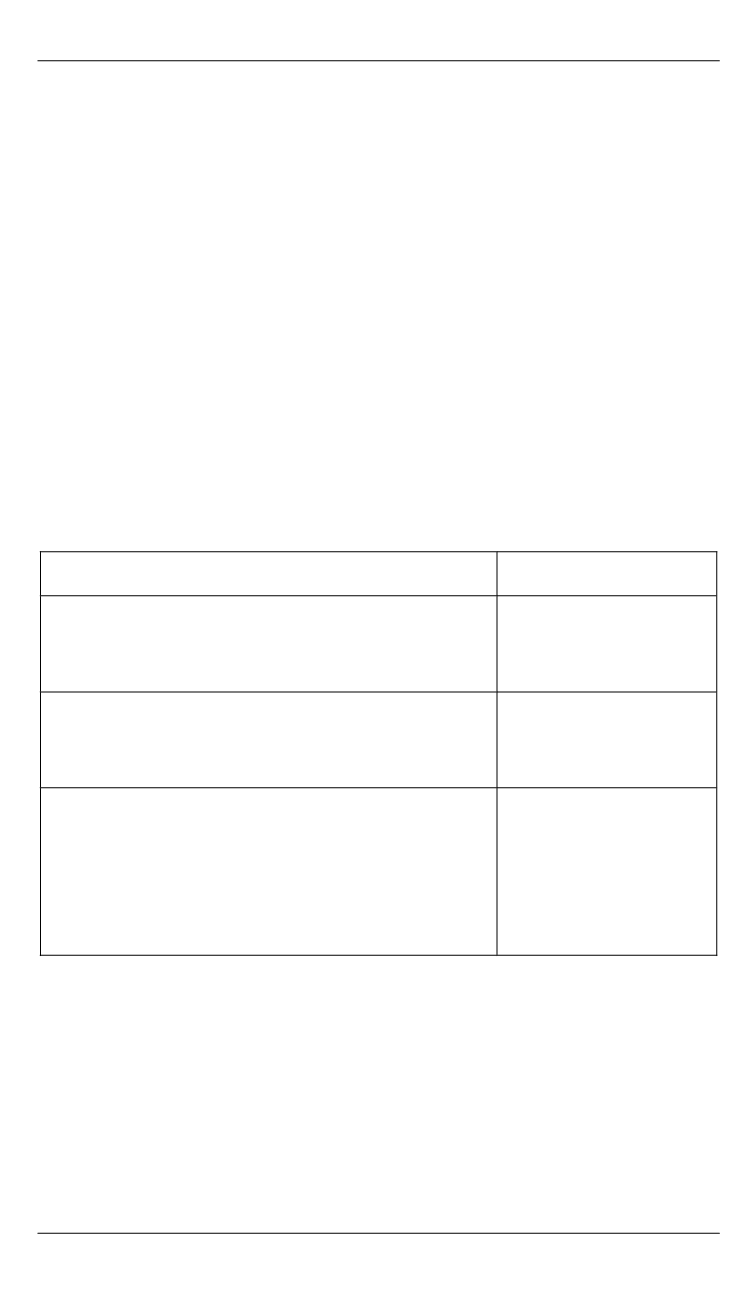
теризующие возможность и целесообразность их формализации:
Группы способов снижения вычислительной
сложности алгоритма
Возможность
формализации
Выбор из альтернативных операций преобразо-
вания графа той, применение которой и провер-
ка условия ее допустимости внесут меньший
вклад в вычислительную сложность алгоритма
Формализация данно-
го способа относится
к области искусствен-
ного интеллекта
Использование рекуррентных процедур, формул
и исключение повторного расчета критериев
и/или оценочных функций
Формализация воз-
можна, но характери-
зуется высокой слож-
ностью
Замена операции объединения множеств конка-
тенацией, использование предикатов, замена
операции на результативно эквивалентную, за-
мена выражений алгебры подмножеств логиче-
ски эквивалентными, замена операции удаления
элемента множества замещением последним или
первым его элементом
Формализация воз-
можна
Оптимизирующие преобразования базируются на результатах
анализа свойств и характеристик графов, их представления в виде
множеств и структур данных, реализующих множества, а также
свойств и количества операций преобразования этих моделей и мно-
жеств.
Как видно из таблицы, в первую очередь целесообразно форма-
лизовать оптимизирующие преобразования третьей группы.
Определение структуры оптимизирующих преобразований.
Реализация того или иного способа снижения вычислительной слож-


