В.А. Овчинников, Г.С. Иванова
10
<Заменяющий фрагмент> ::=
<Элемент множества 1>
<
Множество 1
>
: (
<Элемент множества 1>
<
Множество 1
>
:
<элемент матрицы> := 0,
<Элемент множества 1>
F
1
< Элемент множества 1> :=
Card
(Г <Элемент множества 1>
Г <Элемент множества 1>)),
где <Элемент матрицы> — идентификатор матрицы с соответству-
ющими индексами;
<
Множество 1
>
— идентификатор множества
вершин графа.
Таким образом, для данного преобразования из множества лексем,
полученных при разборе заменяемого фрагмента, можно построить
заменяющий фрагмент. Отсюда следует, что правило оптимизирую-
щего преобразования должно включать только условие существова-
ния: (
A
) (
), где
,
— строки описания заменяемого и за-
меняющего фрагментов;
A
— множество строк описания алгоритма.
Информация, используемая в правилах преобразований, может
быть получена разными способами. Сложность реализации этих спо-
собов, а также полнота имеющихся в описании алгоритма данных
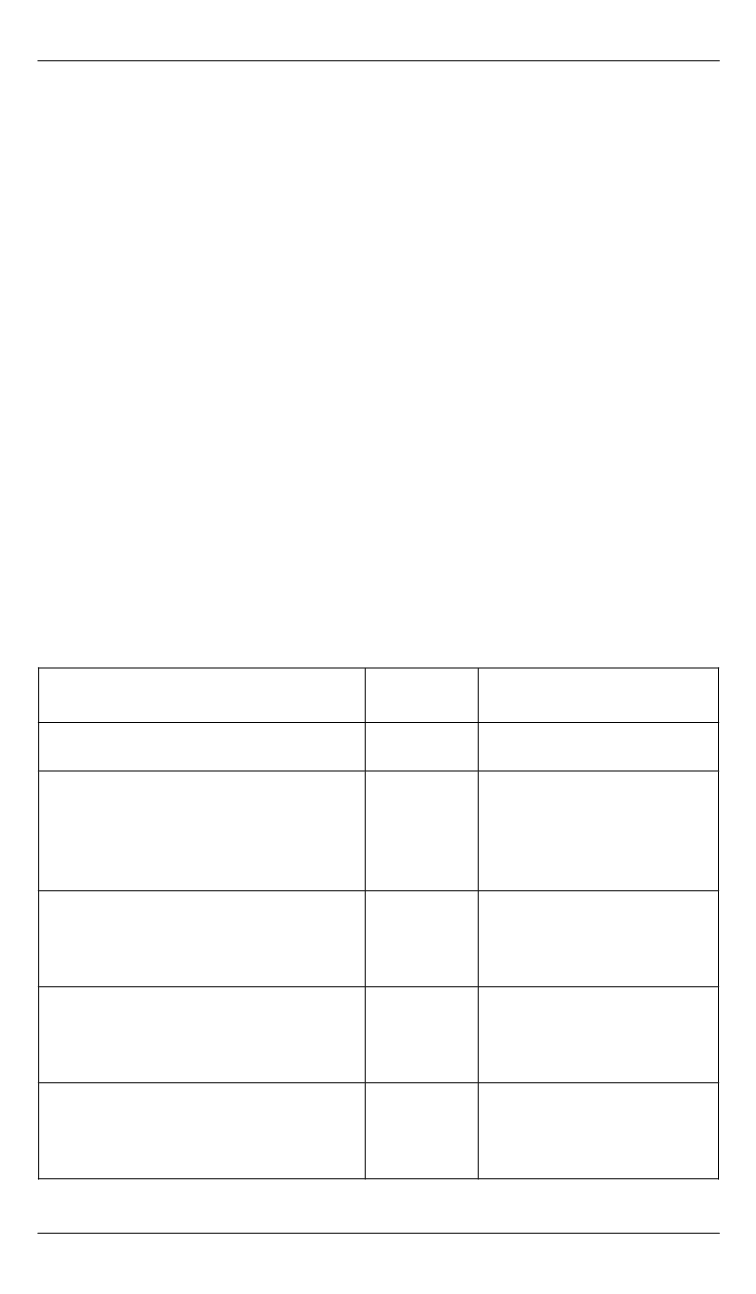
существенно отличаются (см. таблицу).
Характеристика источников и способов получения данных
Источники и способы
получения данных
Сложность
реализации
Полнота данных
Анализ описания алгоритма на
языке операций над множествами
Высокая
100 %
Анализ описания области интер-
претации алгоритма (определение
функций и предикатов, перемен-
ных, множеств, отношений между
ними, размерности)
Средняя
Зависит от разработчика
(без анализа алгоритма
отсутствует информация о
частоте повторения опера-
ций), но может быть 100 %
Анализ описания области интер-
претации алгоритма и описания
алгоритма для определения частот
выполнения операций
Больше
средней
100 %
Система интерактивных запросов о
наличии операций и условий целесо-
образности оптимизирующих преоб-
разований и частот их повторения
Низкая
Зависит от разработчика,
но может быть 100 %
Система интерактивных запросов и
анализ частот выполнения
Меньше
средней
Зависит от разработчика
в меньшей степени, чем у
варианта 4, но может
быть 100 %


