В.В. Девятков, Т.Н. Мьё
4
рые этому множеству не принадлежат, считается равным
! .
e
Мно-
жество нитей
*
?
a
таких, что
{
}
*
*
* *
*
? ? | ? (? )
,
a А a a S
∈
ϕ ∈
будем
обозначать
? .
S
Популярным языком представления процессов является
язык
графов переходов
. Для построения графа переходов процесса счита-
ется, что после каждого его восприятия, в том числе пустого, процесс
осуществляет внутреннюю реакцию или, как говорят, переходит во
внутреннее состояние ожидания следующего восприятия. Находясь
в этом внутреннем состоянии, процесс может порождать внешнюю
реакцию, в том числе пустую. В грáфе переходов каждое состояние
процесса изображается кружком, внутрь которого помещается сим-
вол этого состояния; каждому восприятию соответствует стрелка, со-
единяющая состояния этого перехода. Начальное состояние выделя-
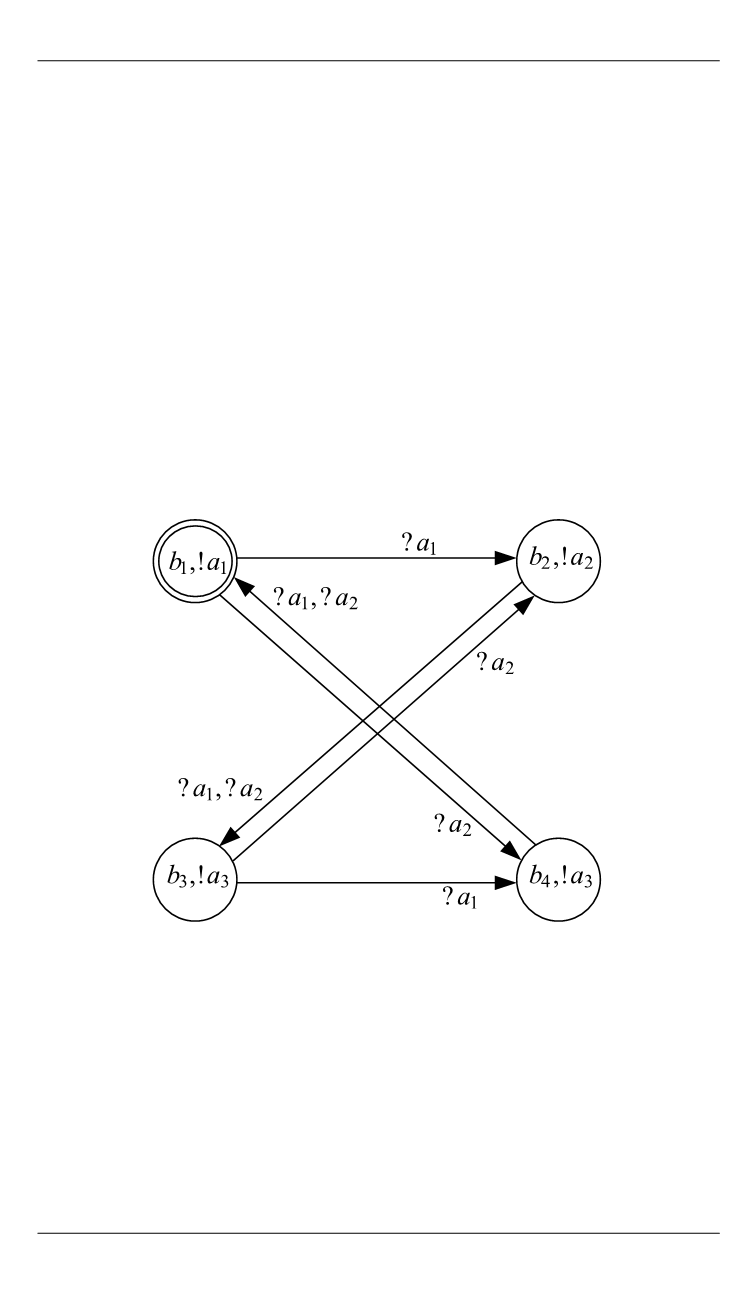
ется двойным кружком. На рис. 1 показан граф переходов некоторого
процесса
P
.
Рис. 1.
Граф переходов процесса
P
Граф переходов процесса позволяет компактно описывать не-
большое множество нитей, в том числе бесконечных. В этих услови-
ях естественным кажется описывать процесс непосредственно его
графом переходов. Однако при большой размерности графа такое
описание становится громоздким и ненаглядным. Альтернативой
этому служит использование адекватных графу канонических про-
цессных выражений, позволяющих легко переходить от графа к этим
выражениям и наоборот.


