

Иерархический метод анализа функционирования программного обеспечения на основе сети Петри - page 8
8
Дуга
шина
х
п
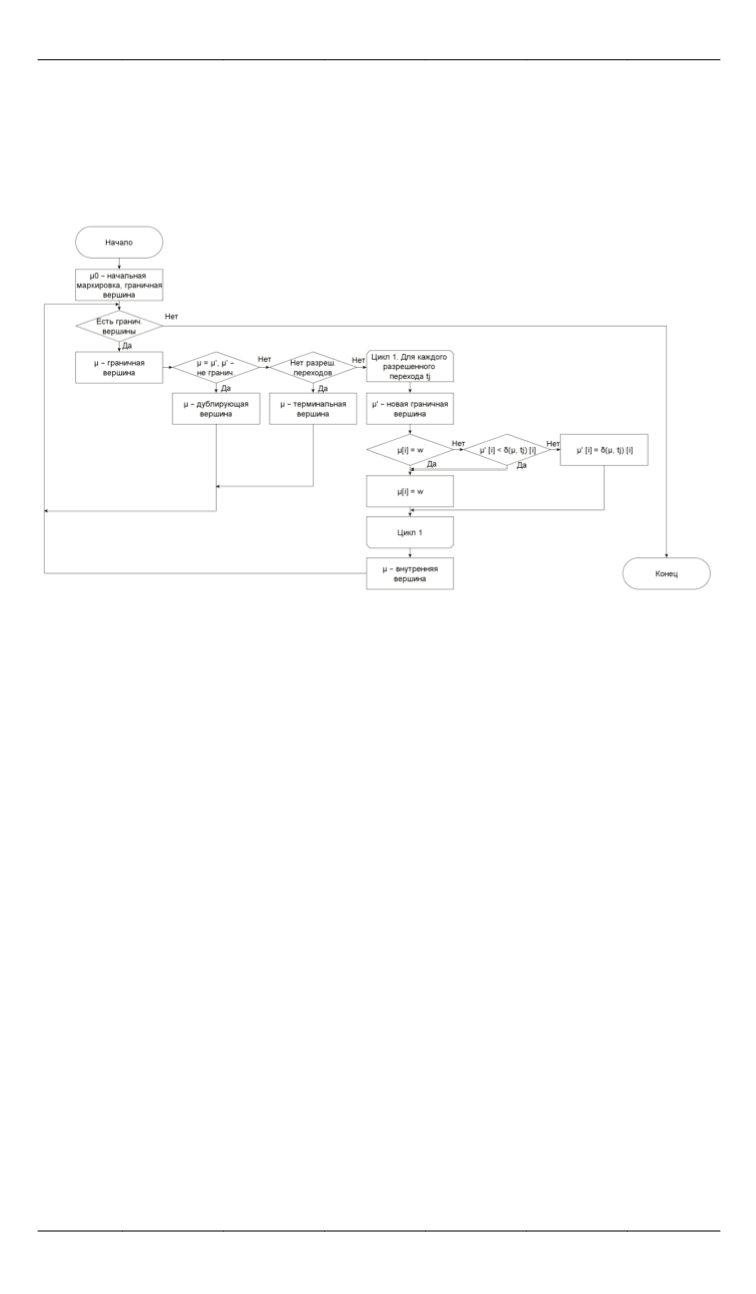
Когда в
внутренн
схема ал
Ри
Особ
обеспече
ся необх
тупиково
конечное
Друг
представ
основыва
ставляющ
имеет
m
зицию).
D
D = D
+
–
Матр
достижим
ствует п
которая п
цательны
След
имеет ре
решения
, помеченн
ереопреде
се вершин
ие, алгор
горитма по
с. 5.
Алгори
енностью
ния, форм
одимость р
й ситуаци
состояние
ой подход
лении и ре
ется на пр
ими вход
строк (по
–
описыва
D
–
— сост
ичная теор
ости. Пус
оследовате
риводит и
м целым р
овательно
шение в н
, тогда
M
′ н
И.В. Руд
ая
t
j
, напр
ляется как
ы дерева
итм остан
строения к
тм построе
данного м
ализованно
азличать у
и. Для это
сети [1].
к анализу
шении мат
едставлен
ную и вых
одной на п
ет входы в
авная матр
ия являетс
ть маркир
льность (в
з
M
0
к
M
'.
ешением с
M
, если
M
′
еотрицател
едостижи
аков
,
А.В. Па
авлена от
внутрення
— терми
авливается
онечного
ния конечн
етода анал
го иерарх
спешное з
го предлаг
сетей Пет
ричных у
ии сети дв
одную фу
ереход) и
переходы
ица измен
я инструм
овка
M
' д
озможно п
Это означ
ледующего
0
M x
′ = +
достижима
ьных цел
ма из
M
0
.
щенкова
вершины
х
я,
z
— ста
нальные,
. На рис.
дерева дос
ого дерева
иза алгори
ической се
авершение
ается ввод
ри основа
равнений.
умя матриц
нкции сет
n
столбцов
,
D
+
— вы
ений.
ентом для
остижима
устая) зап
ает, что
f(G
матрично
D
.
из
M
0
, т
ых. Если у
к вершин
новится гр
дублирую
5 показа
тижимости
достижимос
тма прогр
тью Петри
работы по
ить допол
н на их ма
Матричны
ами
D
–
и
D
и. Каждая
(по одном
ходы из пе
решения п
из
M
0
, тог
усков пере
)
является
го уравнен
огда уравн
равнение
е
z
. Вер-
аничной.
щие или
на блок-
.
ти
аммного
, являет-
дсети от
нительно
тричном
й подход
+
, пред-
матрица
у на по-
реходов.
роблемы
да суще-
ходов
G
,
неотри-
ия для
х
:
(1)
ение (1)
не имеет


