Т.Е. Бояринцева, А.А. Мастихина
6
воположными направлениями, т. е. одним переливанием можно пе-
рейти из одного состояния в другое и обратно.
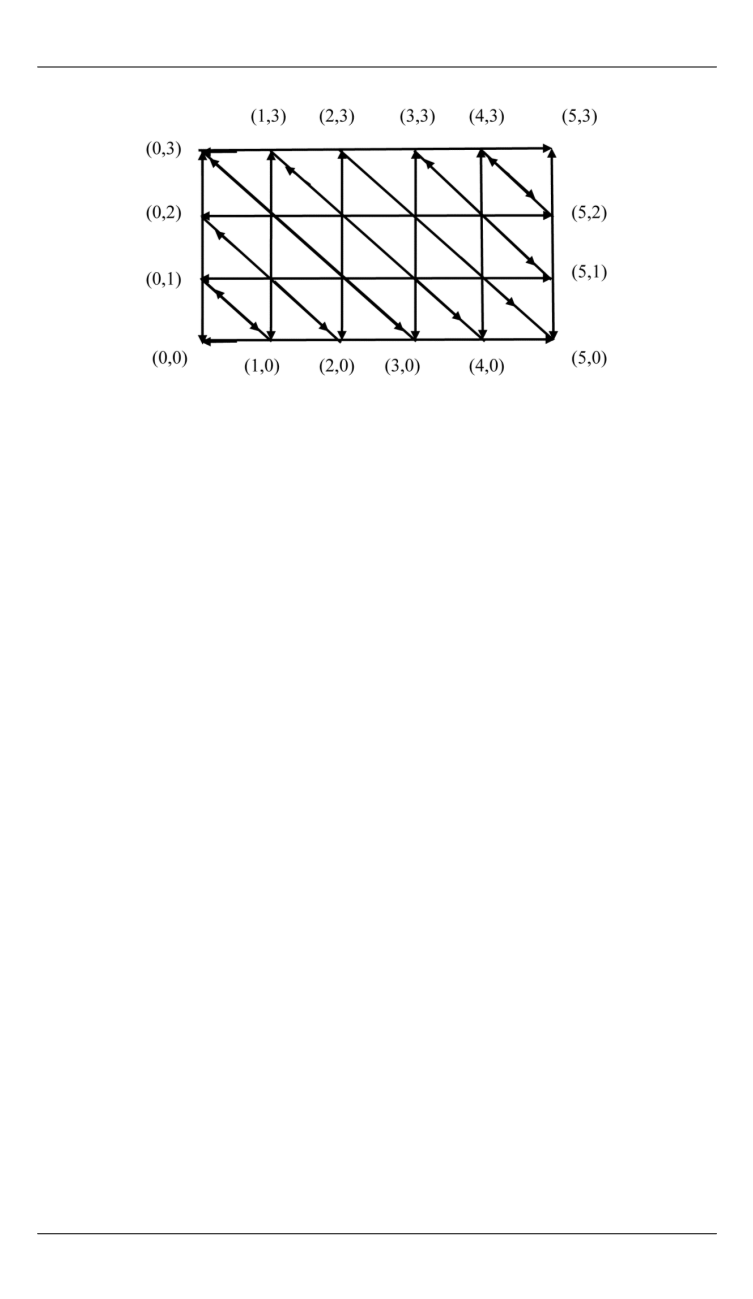
Поиском достижимых вершин можно найти несколько путей, ве-
дущих в (4,0), а также установить, что кратчайшим из них является путь
(0,0)
(5,0)
(2,3)
(2,0)
(0,2)
(5,2)
(4,3)
(4,0).
Также видно, что далеко не все вершины с целыми точками до-
стижимы из (0,0), и ситуация изменится, если начальное состояние
будет какое-либо другое.
2.2. Игра «Открой окна».
На экране вашего компьютера — пря-
моугольник размером
m
n
, разбитый (отрезками прямых) на квад-
ратики размером 1 × 1; квадратики назовем окнами, а множество всех
окон обозначим через
A
. Таким образом,
A
состоит из
mn
окон. Для
любого окна
a
A
обозначим через
T
a
множество окон, находящихся
на той же горизонтали либо на той же вертикали. (Это множество
есть либо крест, либо буква
Т
(возможно, урезанная), либо буква
Г
(она также может оказаться урезанной). Некоторые окна закрыты
(они помечаются крестиком), остальные открыты.
Начинается игра. Подводим курсор к какому-либо окну
a
A
и
нажимаем на мышь. При этом состояние всех окон, входящих в мно-
жество
T
a
, меняется на противоположное (открытые закрываются,
закрытые открываются). Задача состоит в том, чтобы несколькими
нажатиями открыть все окна. Вряд ли вы добьетесь успеха, действуя
наугад. Правильная стратегия состоит в следующем.
Предварительно введем одно определение. Пусть на некотором
этапе игры на экране появляется конфигурация, состоящая из закры-
тых окон. Возьмем произвольное окно
a
A
. Назовем его нечетным,
если число закрытых окон в множестве
T
a
нечетно. Теперь стратегия
описывается крайне просто:
на каждом этапе ваших действий
нажимайте на нечетное окно; если таких окон несколько, нажи-
майте на любое.
Рис. 2.
Граф возможных изменений состояний системы


