Построение двоичного дерева на основе модифицированной схемы хранения…
7
Данный алгоритм создания дерева по схеме LCRS кажется более
сложным для понимания и более объемным для написания, чем алго-
ритм построения двоичного дерева с порядком на «детях», но он яв-
ляется более гибким и легко представимым графически. Кроме того,
можно точно определить, куда будет добавлен новый элемент. Дан-
ное дерево заполняется по уровням слева направо.
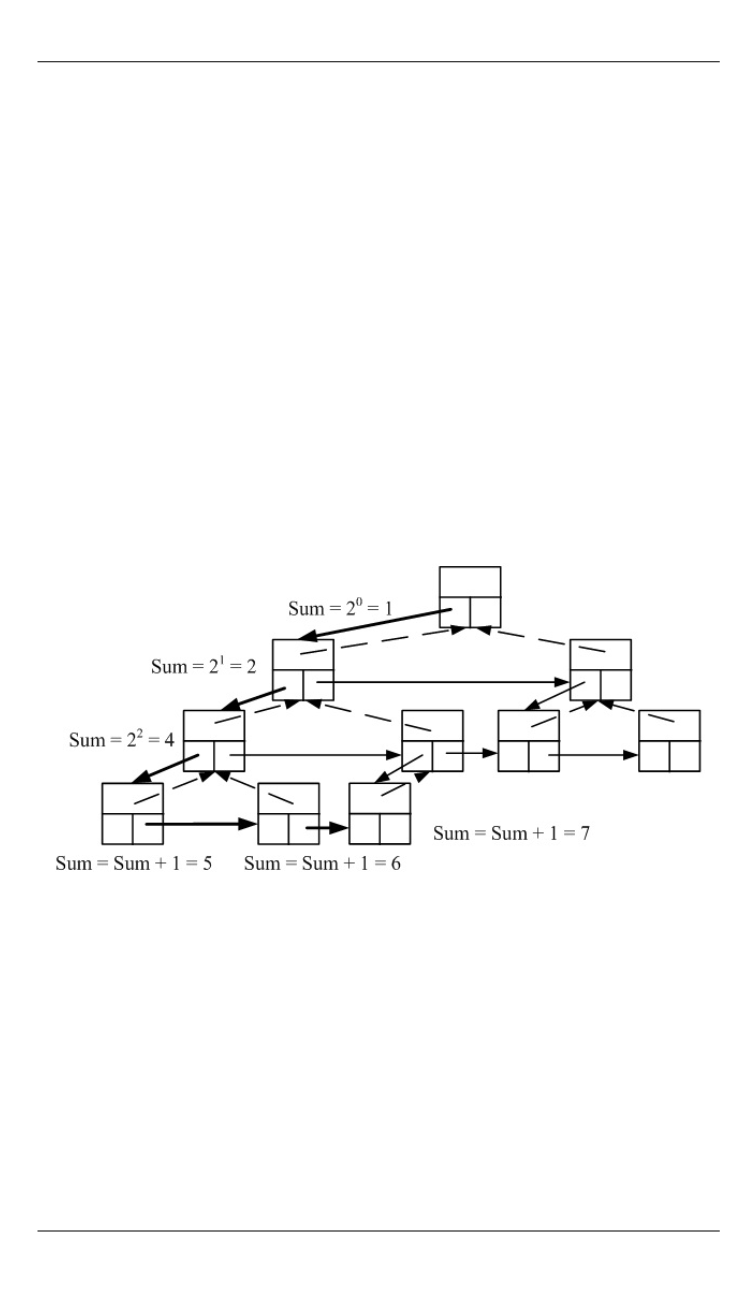
Число узлов дерева LCRS можно легко подсчитать следующим
образом [4]:
1) спуститься по левой ветке дерева (т. е. переходя от вершины к
«правому ребенку») до листового элемента;
2) при каждом переходе к «левому ребенку» номер уровня, на ко-
торый выполнен переход, инкрементируется, а к сумме элементов
прибавляется число «2» в степени, равной данному уровню (нулевым
считать уровень, на котором расположена вершина дерева);
3) на листовом уровне п. 2 не выполняется, а совершается пере-
ход вправо по листовому уровню от самого левого листа до самого
правого, используя поле «правый сосед» каждого листового узла; при
каждом переходе сумма узлов дерева инкрементируется (рис. 6).
Рис. 6.
Схема подсчета числа узлов дерева LCRS
Еще одним преимуществом дерева LCRS является возможность
вывести все элементы
k
-го уровня с помощью несложного алгоритма.
Для этого нужно спуститься по левой ветке дерева до
k
-го уровня и
слева направо вывести все его элементы начиная с текущего, двига-
ясь вправо с помощью поля «правый сосед».
Таким образом, дерево LCRS является одним из нестандартных
решений стандартной задачи о построении двоичного дерева. Дан-
ный подход не лишен недостатков, но, просуммировав все преиму-
щества, можно сделать вывод об эффективности и оправданности его
использования.


