В.В. Горский, М.А. Пугач, В.А. Сысенко
4
число Рейнольдса, рассчитанное по параметрам набегающего на
ударную волну потока воздуха и радиусу сферы
sph
R
.
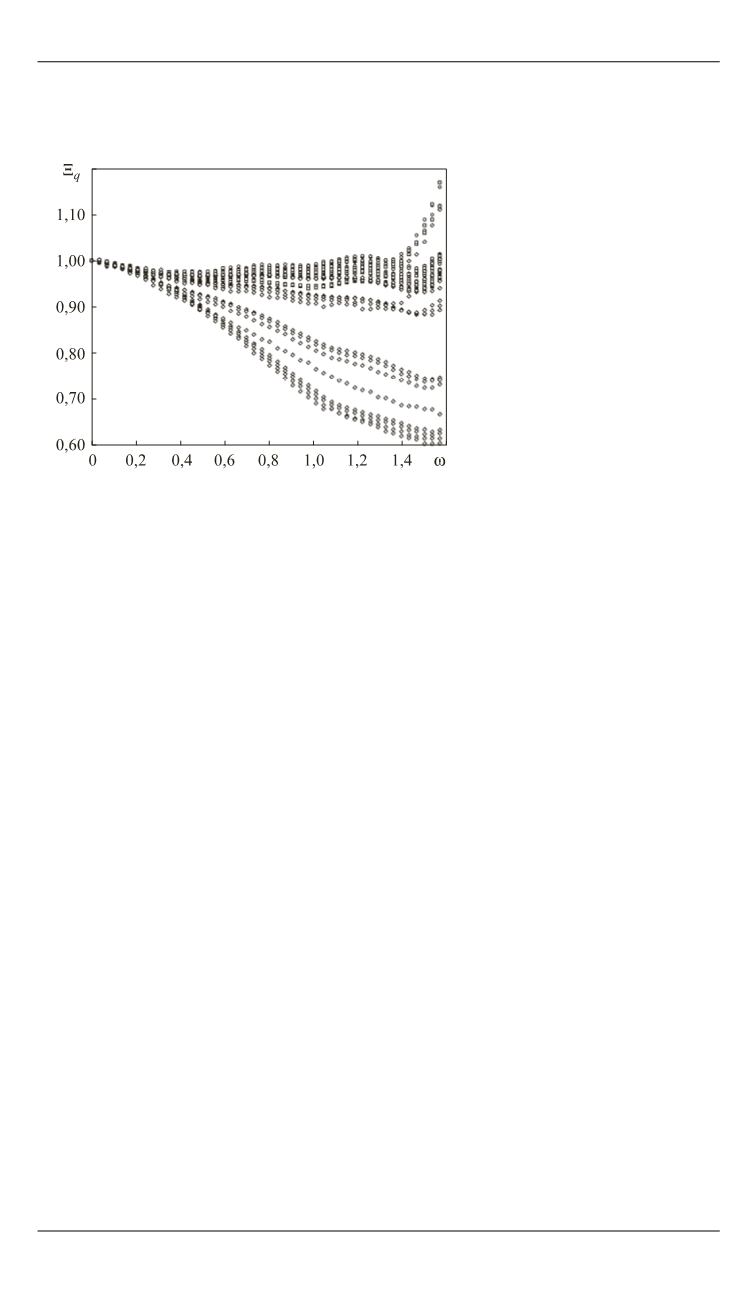
Рис. 1.
Отношение степеней
изменения удельного тепло-
вого потока на непроницае-
мой поверхности полусферы,
обусловленного «эффектом
завихренности», в ее текущем
узле и критической точке:
○ —
3
, ,
Re
10 ;
R sph
□ —
5
10 ,
—
7
10
На базе приведенных данных, полученных при численном реше-
нии уравнений пограничного слоя, предложена следующая аппрок-
симационная формула:
,
Re
, ,
1– M Re
M
q eng
R sph
s =
F
F
+
Re
, ,
M Re
,
q
R sph
+ F
F
(1)
где функция
определена на области ее значений [0, 1]:
3
3
3
1
2
2
cos
1–
cos
cos ;
i
i
i
i
i
i=
i=
i=
=
=
+
(2)
3
1
M
31
M
lg M ;
i–
+i
i=
F
=
(3)
4
1
Re
6
, ,
, ,
1
Re
lg Re
;
i–
+i
R sph
R sph
i=
F
=
(4)
входящие в (2) — (4) аппроксимационные коэффициенты
i
найдены
методом наименьших квадратов [13].
Получены оптимальные значения коэффициентов
i
, определенные
с помощью одного из вариантов эвристического метода прямого поиска
Хука — Дживса [14]:
2
= –0, 083117,
3
= 0, 784108
,
4
= 3, 751927
,
5
= 0, 530707
,
6
= –0,502864
,
7
= –1, 232936
,
8
= 0,868860
,
9
= –0,164345
,
10
= 0, 010117
.


