Алгоритмы решения задачи быстрого поиска
пути на географических картах
7
ществует. Однако у этого алгоритма есть слабая сторона — поиск в
ширину: он игнорирует направление к цели.
Алгоритм «Лучший ― Первый».
Этот эвристический алгоритм
принимает во внимание знания о пространстве поиска для направле-
ния своих усилий. Он похож на алгоритм Дейкстры. Отличие заклю-
чается в том, что узлы в списке оцениваются по приблизительному
оставшемуся расстоянию до цели, кроме того «Лучший ― Первый»
не требует наличия обновлений. Этот алгоритм достаточно быстрый
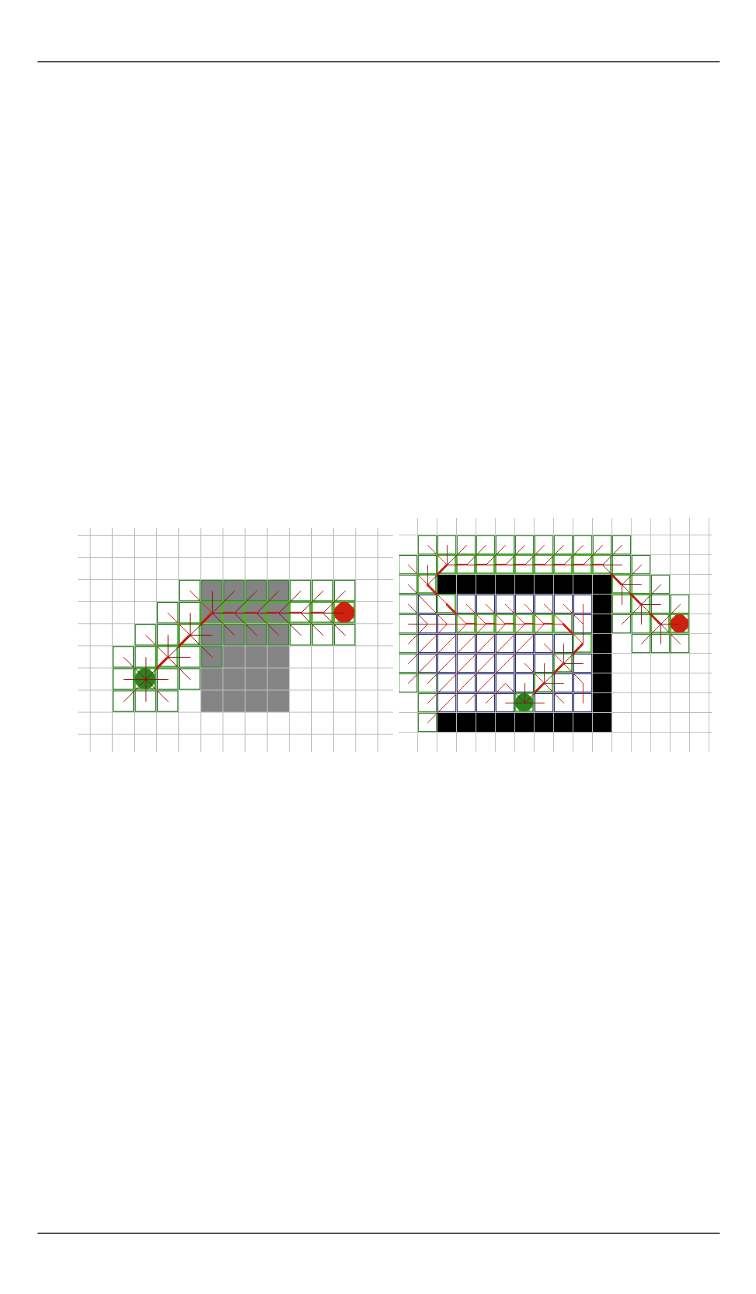
и направляется по прямой к цели, однако он имеет и недостатки. На
рис. 1,
а
показано, что он не принимает во внимание накопленную
стоимость пути, направляясь по прямой через труднопроходимую
зону. На рис. 1,
б
можно увидеть, что найденный путь изгибается во-
круг препятствия аналогично пути, полученному алгоритмом трасси-
ровки. Недостатком является и то, что вершина, до которой ищется
путь, может оказаться в поддереве, рассматриваемом в последнюю
очередь.
а
б
Рис. 1.
Иллюстрация работы алгоритма «Лучший — Первый»:
зеленый маркер — начало пути; красный маркер — конец пути;
зеленый контур — анализируемые ячейки; красные линии —
труднопроходимая зона; черные ячейки — непроходимая зона.
Эвристические алгоритмы определения субоптимального
пути.
Субоптимальные алгоритмы работают по принципу
пошагового улучшения текущего результата. Выбирается некоторая
эвристическая функция, с ее помощью на каждом шаге можно
выбрать ячейку сетки, расстояние от которой до конечной точки
будет иметь минимальное значение (на основании значения эвристи-
ческой функции). Преимуществом подобных алгоритмов является
меньшее количество используемых ресурсов по сравнению с ал-
горитмами определения оптимального пути. Многие эвристические
алгоритмы позволяют выдать точку, являющуюся предположительно
наиболее близкой к конечной, и маршрут до нее, что важно для


