В.В. Девятков, Д.В. Ошкало
4
жество всех внешних реакций процесса
P
, включая пустую внешнюю
реакцию
!e
;
S
— множество всех нитей, выполняемых процессом
P
,
таких что
*
,
S ?A !A
*
?A
— множество всех нитей
*
?a
в алфавите
.
?A
Будем обозначать
( )
P S
процесс
P
, выполняющий множество ни-
тей
* * *
( )
?a ?a S
, где
*
— функция на множестве
*
?A
, которая
ставит в соответствие каждой нити
*
*
?a ?A
внешнюю реакцию из
множества
.
!A
Значение функции
*
на нитях множества
*
?A
, на ко-
торых эта функция не определена и которые этому множеству не
принадлежат, считается равным
!e
. Множество нитей
*
?a
, таких что
*
* * * *
|
( )
?a ?A ?a ?a S
, будем обозначать
.
?S
Популярным языком представления процессов является язык
графов переходов. При построении графа переходов процесса счита-
ется, что после каждого его восприятия, в том числе пустого, процесс
осуществляет внутреннюю реакцию или, как говорят, переходит во
внутреннее состояние ожидания следующего восприятия. Находясь в
этом внутреннем состоянии, процесс может порождать внешнюю ре-
акцию, в том числе пустую. В графе переходов каждое состояние
процесса изображается в виде кружка, внутри которого — символ
этого состояния; каждому восприятию соответствует стрелка, соеди-
няющая состояния этого перехода. Начальное состояние выделяется
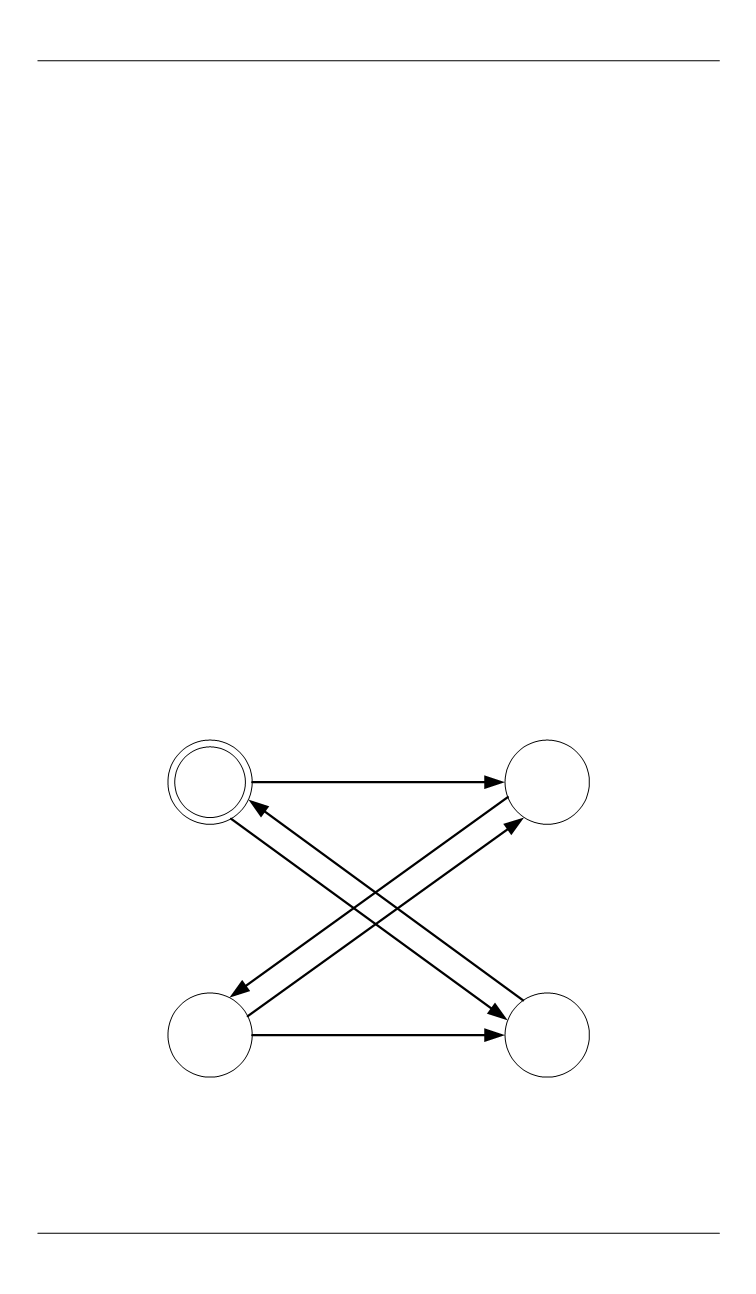
двойным кружком. На рис. 1 показан граф переходов некоторого
процесса
P
.
b
1
,
!a
1
b
2
,
!a
2
b
3
,
!a
3
b
4
,
!a
3
?a
1
?a
1
?a
2
?a
2
?a
1
,
?a
2
?a
1
,
?a
2
Рис. 1.
Граф переходов процесса
P
Граф переходов процесса позволяет компактно описывать не-
большое множество нитей, в том числе бесконечных. В этих услови-


