В.А. Овчинников
2
ный и преобразованный алгоритмы должны быть
эквивалентны
, т. е.
на всех допустимых наборах входных данных задачи давать одинако-
вые результаты.
Классификация рассматриваемых способов снижения вы-
числительной сложности.
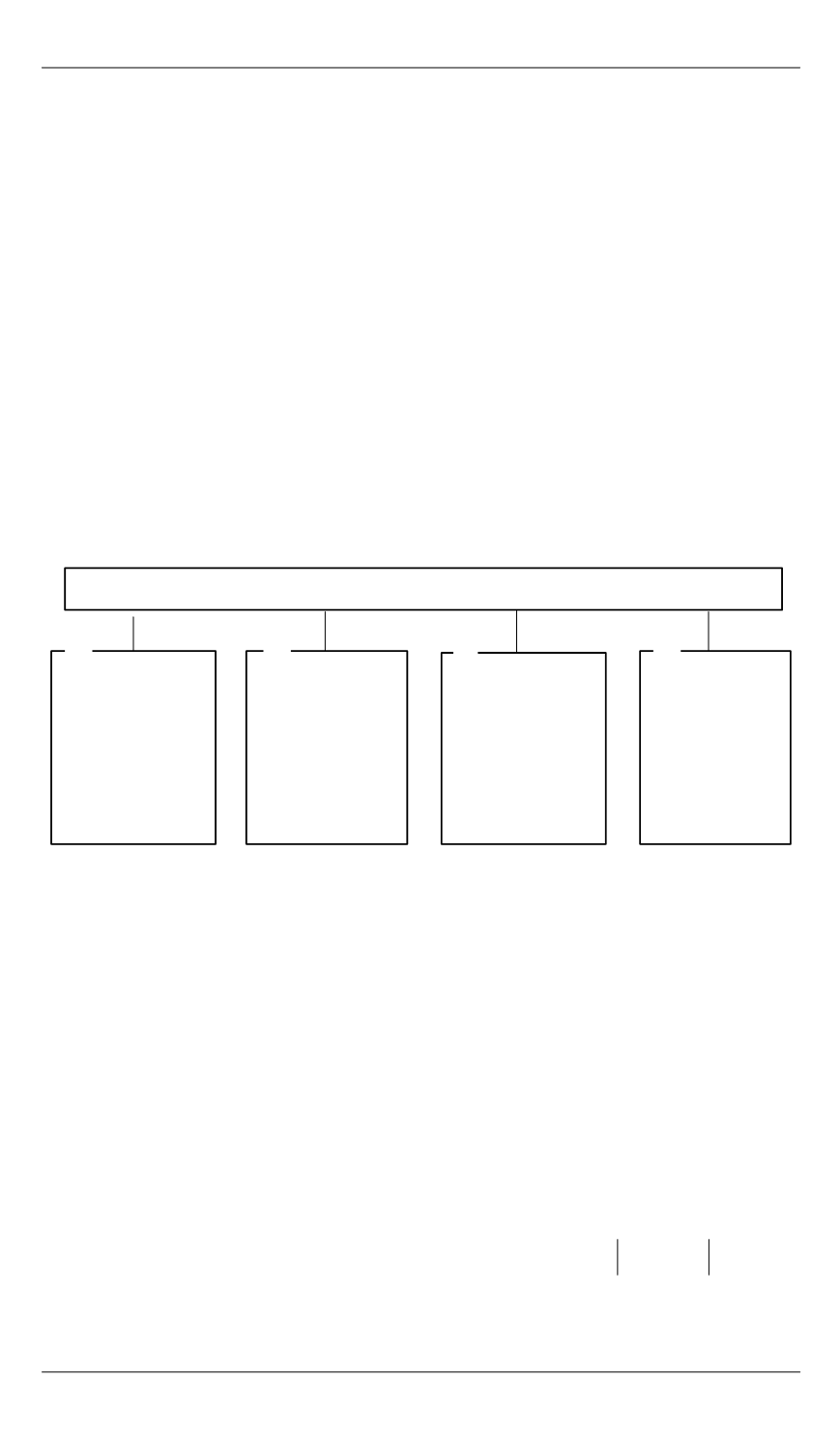
Предлагаемые автором способы преобра-
зования алгоритмов показаны на рис. 1. Возможность использования
первых двух из указанных способов обусловлена также ограниченно-
стью количества элементов, связанных с добавляемым/удаляемым
компонентом при пошаговом формировании графа-результата. Третье
и четвертое преобразование заключаются в замене операций над
множествами на более эффективные, причем такая замена возможна
при выполнении определенных условий.
В качестве примеров будет рассмотрена ограниченная выборка
возможных применений указанных способов. Объектами преобразо-
ваний в примерах будут графы, описанные в [1–4].
Использование
рекуррентных
формул для
расчёта
критериев
1
Применение
рекуррентных
процедур для
формирования
множеств
2
3
4
1
2
1 2
1
2
Замена операции
на
, ecли
X X X
X X X
X X
= ∪
= ⋅
∩ = ∅
Способы преобразования алгоритмов
2
1
2
2
1
1
Замена операции
\
на
\ ,
ecли
i
i
X X X
X X X
X X X
=
=
= ⋅
Рис. 1.
Способы преобразования алгоритмов, вытекающие из принципа
последовательного формирования решения
Способы, использующие рекуррентные формулы.
Первый
способ
— применение рекуррентных формул для определения новых
значений критериев и/или оценочных функций. В качестве примера
рассмотрим алгоритм итерационного улучшения начального разреза-
ния гиперграфа
H
(
X
,
U
) парными перестановками вершин [2]. Крите-
рий оптимальности — минимум количества ребер
S
, попадающих в
разрез. Пусть имеется начальная компоновка схемы на две подсхемы.
Соответственно ее модель — гиперграф
H
(
X
,
U
) — разрезана на два кус-
ка
(
)
0 0
1 1 1
,
H X U
и
(
)
0 0
2 2 2
,
H X U
, где верхний индекс «0» обозначает шаг
обмена и
0
0
1
2
,
X X X
∪ =
0
0
1
2
,
X X
∩ = ∅
0
0
1
2
,
U U U
∪ =
0
0
0
1
2
U U S
∩ =
,
S
0
— количество ребер, соединяющих эти куски. Поскольку операцией пре-
образования разрезания гиперграфа является обмен вершинами между


