Инженерная методика оценки компьютерных систем
3
оптимальная КС из набора
1
, ...,
N
S
S
для решения поставленной
задачи, т. е.
k
S S
, если выполняется следующее равенство
1 2
max ,
, ...,
, 1
.
k
N
D
D D D k N
(1)
Равенство (1) сформулировано в предположении, что дефицит
одного ресурса может быть скомпенсирован избытком другого [4, 8,
9]. Если некоторый ресурс не должен опускаться ниже определенно-
го уровня (критический дефицит), то выражение (1) необходимо до-
полнить соответствующими неравенствами.
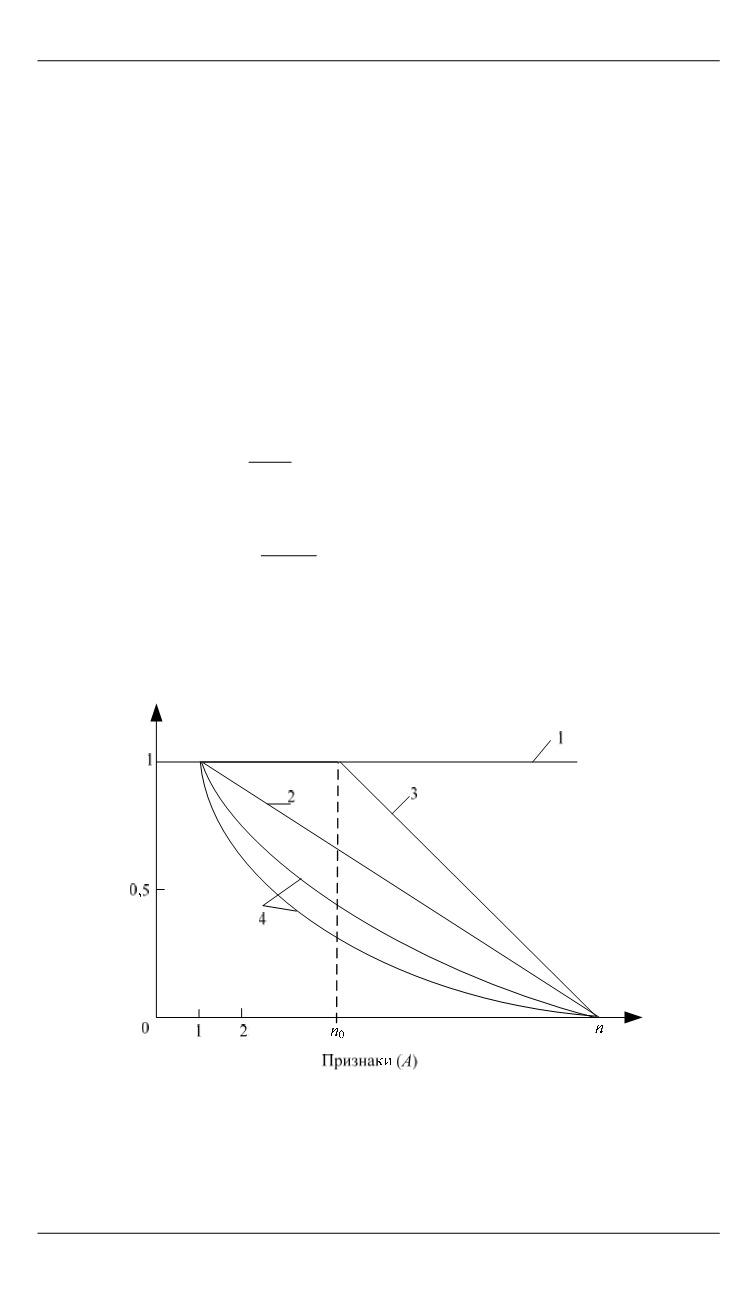
Присвоение весов признакам.
Предположим, что весовая функ-
ция относится к одному из четырех классов, указанных на рис. 2:
• класс 1:
1
i
w
;
• класс 2:
1 1
, 1
1
i
i
w
i n
n
;
• класс 3:
0
0
0
0
1, 1
,
1
,
;
i
i n n
w i n n i n
n n
• класс 4:
*
1
, 1
,
c i
i
w e
i n
где
*
0
с
— масштабный параметр.
Вес (
w
)
Рис. 2.
Классы весовых функций
Взвешенные разности
l
D
для этих классов весовых функций
имеют следующий вид:


